【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 为菱形,且
为菱形,且![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点.
中点.
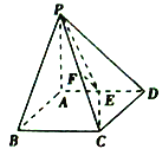
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)求证:平面![]() 平面
平面![]() .
.
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】【试题分析】(1)借助题设与已知条件运用等价转化的数学思想将点到面的距离转化为另一个点到平面的距离;(2)依据题设条件,先运用线面垂直的判定定理证明线面垂直,进而运用面面垂直的判定定理证明面面垂直。
(1)解:如图,
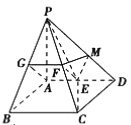
取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
因为底面![]() 为菱形,且
为菱形,且![]() ,
,![]() ,
,
所以底面![]() 为正方形.
为正方形.
∵![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,
中点,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 且
且![]() ,∴四边形
,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等,即距离为
的距离相等,即距离为![]() .
.
(2)证明:由(1)知![]() ,
,![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() ,又∵
,又∵![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
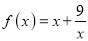 (
(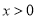 ).
).(1)判断函数
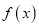 在
在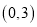 和
和 的单调性,并用定义证明
的单调性,并用定义证明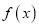 在
在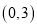 上的单调性;
上的单调性;(2)若函数
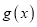 是定义域为
是定义域为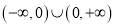 的偶函数,且
的偶函数,且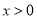 时,
时,  ,
,①当
 时,写出
时,写出 的表达式;
的表达式;②若函数
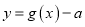 有四个零点,写出
有四个零点,写出 的取值范围(不需要说明理由).
的取值范围(不需要说明理由). -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=
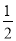 ﹣p
﹣p④回归直线一定过样本点的中心(
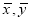 ).
).其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
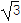 sinωx·cosωx-cos2ωx(ω>0)的最小正周期为
sinωx·cosωx-cos2ωx(ω>0)的最小正周期为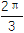 .
.(1)求ω的值;
(2)在△ABC中,sinB,sinA,sinC成等比数列,求此时f(A)的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案
不善于使用学案
总计
学习成绩优秀
40
学习成绩一般
30
总计
100
参考公式:
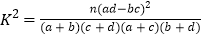 ,其中
,其中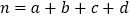 .
.参考数据:
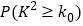
0.050
0.010
0.001
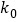
3.841
6.635
10.828
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)若从学习成绩优秀的同学中随机抽取10人继续调查,采用何种方法较为合理,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“菊花”型烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂.通过研究,发现该型烟花爆裂时距地面的高度
 (单位:米)与时间
(单位:米)与时间 (单位:秒)存在函数关系,并得到相关数据如表:
(单位:秒)存在函数关系,并得到相关数据如表:时间

1


高度




(1)根据表中数据,从下列函数中选取一个函数描述该型烟花爆裂时距地面的高度
 与时间
与时间 的变化关系:
的变化关系:  ,
,  ,
,  ,确定此函数解析式并简单说明理由;
,确定此函数解析式并简单说明理由;(2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求此时烟花距地面的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
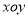 中,直线
中,直线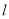 的参数方程为
的参数方程为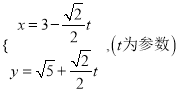 。在以原点
。在以原点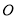 为极点,
为极点, 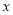 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆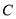 的方程为
的方程为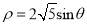 。
。(1)写出直线
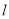 的普通方程和圆
的普通方程和圆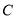 的直角坐标方程;
的直角坐标方程;(2)若点P坐标为
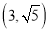 ,圆
,圆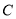 与直线
与直线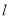 交于
交于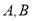 两点,求
两点,求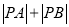 的值。
的值。
相关试题

