【题目】(本小题满分12分)已知数列![]() 和
和![]() 满足
满足![]() ,若
,若![]() 为等比数列,且
为等比数列,且![]() ,
,![]() .
.
(1)求![]() 与
与![]() ;
;
(2)设![]() (
(![]() ),记数列
),记数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
(I)求![]() ;
;
(II)求正整数![]() ,使得对任意
,使得对任意![]() 均有
均有![]() .
.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)(I)
;(2)(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(1)由![]()
![]() 求得
求得![]() ,又
,又![]() 且数列
且数列![]() 为等比数列,可求出公比,从而可求数列
为等比数列,可求出公比,从而可求数列![]() 的通项公式,由
的通项公式,由![]() 可求数列
可求数列![]() 的通项公式;
的通项公式;
(2)(I)数列![]() 是等比数列,又因为
是等比数列,又因为![]() ,所以
,所以![]() ,求数列
,求数列![]() 的前
的前![]() 项和为
项和为![]() 时先分组,再用等比数列的求和公式及裂项相消法求之即可;(II)由数列
时先分组,再用等比数列的求和公式及裂项相消法求之即可;(II)由数列![]() 的通项公式可知,
的通项公式可知,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 的最大值为
的最大值为![]() ,故使
,故使![]() 成立的正整数
成立的正整数![]() .
.
试题解析:(1)由题意,可知![]()
![]() ,
,
所以可得![]() ,
,
又由![]() ,得公比
,得公比![]() (
(![]() 舍去)
舍去)
所以数列![]() 的通项公式为
的通项公式为![]()
![]() ,
,
所以![]() ,
,
故数列![]() 的通项公式为
的通项公式为![]()
![]()
(2)(I)由(1)知,![]()
![]() ,
,
所以![]()
![]() .
.
(II)因为![]()
当![]() 时,
时,![]() ,
,
而![]() ,
,
得![]() ,
,
所以当![]() 时,
时,![]()
综上,若对任意![]() 均有
均有![]() ,则
,则![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某中学高一学生的数学与地理的水平测试成绩抽样统计如下表:若抽取的学生数为
 ,成绩分为
,成绩分为 (优秀)、
(优秀)、 (良好)、
(良好)、 (及格)三个等级,设
(及格)三个等级,设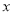 ,
,  分别表示数学成绩与地理成绩.例如:表中地理成绩为
分别表示数学成绩与地理成绩.例如:表中地理成绩为 等级的共有
等级的共有 人,数学成绩为
人,数学成绩为 级且地理成绩为
级且地理成绩为 等级的有8人.已知
等级的有8人.已知 与
与 均为
均为 等级的频率是0.07.
等级的频率是0.07.(1)设在该样本中,数学成绩优秀率是
 ,求
,求 ,
,  的值;
的值;(2)已知
 ,
,  ,求数学成绩为
,求数学成绩为 等级的人数比数学成绩为
等级的人数比数学成绩为 等级的人数多的概率.
等级的人数多的概率.
人数





14
40
10


36


28
8
34
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
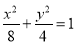 ,过点
,过点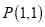 作直线
作直线 与椭圆交于
与椭圆交于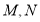 两点.
两点.(1)若点
 平分线段
平分线段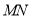 ,试求直线
,试求直线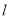 的方程;
的方程;(2)设与满足(1)中条件的直线
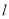 平行的直线与椭圆交于
平行的直线与椭圆交于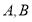 两点,
两点,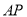 与椭圆交于点
与椭圆交于点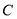 ,
,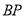 与椭圆交于点
与椭圆交于点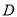 ,求证:
,求证: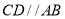 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为
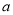 ,再由乙猜甲刚才想的数字把乙想的数字记为
,再由乙猜甲刚才想的数字把乙想的数字记为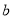 ,且
,且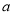 ,
, 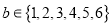 ,记
,记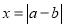 .
.(1)求
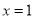 的概率;
的概率;(2)若
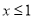 ,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率. -
科目: 来源: 题型:
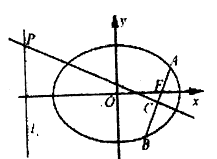
查看答案和解析>>【题目】如图,在平面直角坐标系
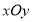 中,已知椭圆
中,已知椭圆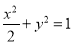 ,直线
,直线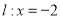 ,过右焦点
,过右焦点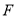 的直线与椭圆交于
的直线与椭圆交于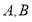 两点,线段
两点,线段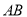 的垂直平分线分别交直线
的垂直平分线分别交直线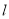 和
和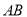 于点
于点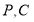 .
.
(1)求弦长
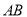 的最小值;
的最小值;(2)在直线
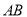 上任取一点
上任取一点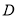 ,当
,当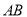 的斜率
的斜率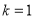 时,求
时,求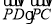 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.

(1) 证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位有200名职工,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是
相关试题

