【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为![]() ,再由乙猜甲刚才想的数字把乙想的数字记为
,再由乙猜甲刚才想的数字把乙想的数字记为![]() ,且
,且![]() ,
, ![]() ,记
,记![]() .
.
(1)求![]() 的概率;
的概率;
(2)若![]() ,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:由甲任想一个数字记为![]() ,由乙猜甲刚才想的数字,得到
,由乙猜甲刚才想的数字,得到![]() ,
, ![]()
得到基本事件总数,
(1)列出![]() 包含的基本事件的个数,即可利用古典概型求解概率;
包含的基本事件的个数,即可利用古典概型求解概率;
(2)列出![]() 包含的基本事件的个数,即可求解 “甲乙心有灵犀”的概率.
包含的基本事件的个数,即可求解 “甲乙心有灵犀”的概率.
试题解析:
由甲任想一个数字记为![]() ,再由乙猜甲刚才想的数字,
,再由乙猜甲刚才想的数字,
把乙想的数字记为![]() ,且
,且![]() ,
, ![]()
![]()
基本事件总数![]() ,(列表或树状图)
,(列表或树状图)
(1)![]() 包含的基本事件有:
包含的基本事件有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共10个,
共10个,
![]() 的概率
的概率![]() .
.
(2)![]() 包含的基本事件有:
包含的基本事件有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共16个,
共16个,
![]() “甲乙心有灵犀”的概率
“甲乙心有灵犀”的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学利用国庆节进行社会实践,对
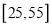 岁的人群随机抽取
岁的人群随机抽取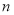 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:组数
分组
低碳族的人数
占本组的频率
第一组
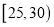
120
0.6
第二组

195
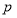
第三组
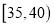
100
0.5
第四组
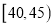
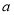
0.4
第五组
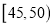
30
0.3
第六组

15
0.3
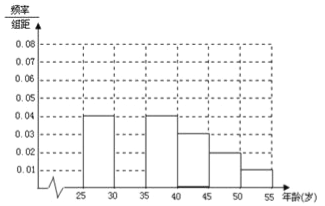
(1)补全频率分布直方图并求
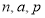 的值(直接写结果);
的值(直接写结果);(2)从年龄段在
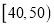 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在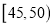 岁的概率.
岁的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某中学高一学生的数学与地理的水平测试成绩抽样统计如下表:若抽取的学生数为
 ,成绩分为
,成绩分为 (优秀)、
(优秀)、 (良好)、
(良好)、 (及格)三个等级,设
(及格)三个等级,设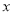 ,
,  分别表示数学成绩与地理成绩.例如:表中地理成绩为
分别表示数学成绩与地理成绩.例如:表中地理成绩为 等级的共有
等级的共有 人,数学成绩为
人,数学成绩为 级且地理成绩为
级且地理成绩为 等级的有8人.已知
等级的有8人.已知 与
与 均为
均为 等级的频率是0.07.
等级的频率是0.07.(1)设在该样本中,数学成绩优秀率是
 ,求
,求 ,
,  的值;
的值;(2)已知
 ,
,  ,求数学成绩为
,求数学成绩为 等级的人数比数学成绩为
等级的人数比数学成绩为 等级的人数多的概率.
等级的人数多的概率.
人数





14
40
10


36


28
8
34
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
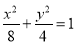 ,过点
,过点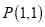 作直线
作直线 与椭圆交于
与椭圆交于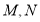 两点.
两点.(1)若点
 平分线段
平分线段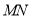 ,试求直线
,试求直线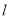 的方程;
的方程;(2)设与满足(1)中条件的直线
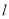 平行的直线与椭圆交于
平行的直线与椭圆交于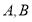 两点,
两点,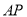 与椭圆交于点
与椭圆交于点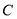 ,
,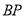 与椭圆交于点
与椭圆交于点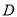 ,求证:
,求证: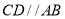 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)已知数列
 和
和 满足
满足 ,若
,若 为等比数列,且
为等比数列,且 ,
, .
.(1)求
 与
与 ;
;(2)设
 (
( ),记数列
),记数列 的前
的前 项和为
项和为 ,
,(I)求
 ;
;(II)求正整数
 ,使得对任意
,使得对任意 均有
均有 .
. -
科目: 来源: 题型:
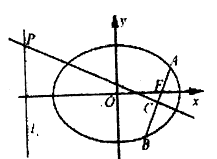
查看答案和解析>>【题目】如图,在平面直角坐标系
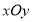 中,已知椭圆
中,已知椭圆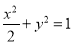 ,直线
,直线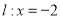 ,过右焦点
,过右焦点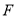 的直线与椭圆交于
的直线与椭圆交于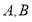 两点,线段
两点,线段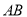 的垂直平分线分别交直线
的垂直平分线分别交直线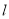 和
和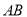 于点
于点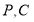 .
.
(1)求弦长
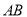 的最小值;
的最小值;(2)在直线
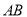 上任取一点
上任取一点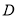 ,当
,当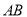 的斜率
的斜率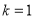 时,求
时,求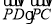 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.

(1) 证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
相关试题

