【题目】在△ABC中,已知AB=2,cosB= ![]() (Ⅰ)若AC=2
(Ⅰ)若AC=2 ![]() ,求sinC的值;
,求sinC的值;
(Ⅱ)若点D在边AC上,且AD=2DC,BD= ![]() ,求BC的长.
,求BC的长.
参考答案:
【答案】解:(Ⅰ)∵cosB= ![]() , ∴sinB=
, ∴sinB= ![]() =
= ![]() ,
,
∵ ![]() ,且AC=2
,且AC=2 ![]() ,AB=2,
,AB=2,
∴sinC= ![]() =
= ![]()
(Ⅱ)在△ABC中,设BC=a,AC=b,
∵AB=2,cosB= ![]() ,
,
∴由余弦定理可得:b2=a2+4﹣ ![]() ,①
,①
在△ABD和△BCD中,由余弦定理可得:
cos∠ADB= 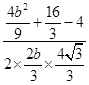 ,cos∠BDC=
,cos∠BDC= 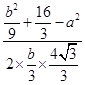 ,
,
∵cos∠ADB=﹣cos∠BDC,
∴ 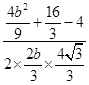 =﹣
=﹣ 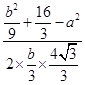 ,解得:
,解得: ![]() ﹣a2=﹣6,②
﹣a2=﹣6,②
∴由①②可得:a=3,b=3,即BC的值为3
【解析】(Ⅰ)由已知利用同角三角函数基本关系式可求sinB,利用正弦定理即可解得sinC的值.(Ⅱ)在△ABC中,设BC=a,AC=b,由余弦定理可得:b2=a2+4﹣ ![]() ,①,由于cos∠ADB=﹣cos∠BDC,利用余弦定理可得
,①,由于cos∠ADB=﹣cos∠BDC,利用余弦定理可得 ![]() ﹣a2=﹣6,②,联立即可得解BC的值.
﹣a2=﹣6,②,联立即可得解BC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频举分布直方图都受到不同程度的破坏,可见部分
如下.


(1)求全班人数及分数在
 内的频数;
内的频数;(2)估计该班的平均分数,并计算频率分布直方图中
 的矩形的高;
的矩形的高;(3)若要从分数在
 内的试卷中任取两份分析学生的失分情况,在抽取的试卷中,求至少有一份分数在
内的试卷中任取两份分析学生的失分情况,在抽取的试卷中,求至少有一份分数在 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=﹣
 sinx
sinx  cosx+1 (Ⅰ)求函数f(x)的最小正周期和单调递增区间;
cosx+1 (Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)若x∈[0, ],且f(x)=
],且f(x)=  ,求cosx的值.
,求cosx的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相邻整数的概率;
(Ⅱ)求取出的两个球上标号之和能被3整除的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an]的前n项和记为Sn , 且满足Sn=2an﹣n,n∈N* (Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明: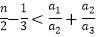 +…
+… 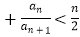 (n∈N*)
(n∈N*) -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
年份200x(年)
0
1
2
3
4
人口数y(十)万
5
7
8
11
19
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出Y关于x的线性回归方程Y=bx+a;
(3)据此估计2005年该城市人口总数. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆C:
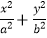 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为  ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 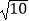 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.
相关试题

