【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最值;
上的最值;
(2)讨论函数![]() 的单调性;
的单调性;
(3)当![]() 时,有
时,有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ,
, ![]() ;(2)当
;(2)当![]() 时,
时, ![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时, ![]() 在
在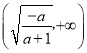 单调递增,在
单调递增,在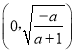 上单调递减,当
上单调递减,当![]() 时,
时, ![]() 在
在![]() 单调递减;(3)
单调递减;(3) ![]() .
.
【解析】试题分析:(1)![]() 在
在![]() 的最值只能在
的最值只能在![]() 和区间的两个端点取到,因此,通过算出上述点并比较其函数值可得函数
和区间的两个端点取到,因此,通过算出上述点并比较其函数值可得函数![]() 在
在![]() 的最值;(2)算出
的最值;(2)算出![]() ,对
,对![]() 的取值范围分情况讨论即可;(3)根据(2)中得到的单调性化简不等式,从而求解不等式,解得
的取值范围分情况讨论即可;(3)根据(2)中得到的单调性化简不等式,从而求解不等式,解得![]() 的取值范围.
的取值范围.
试题解析:(1)当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
∵![]() 的定义域为
的定义域为![]() ,∴由
,∴由![]() ,得
,得![]() .……………………2分
.……………………2分
∴![]() 在区间
在区间![]() 上的最值只可能在
上的最值只可能在![]() 取到,
取到,
而![]() ,
, ![]() ,
, ![]() ,……4分
,……4分
(2)![]() ,
, ![]() ,
,
①当![]() ,即
,即![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递减;……5分
上单调递减;……5分
②当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增;…………………………6分
上单调递增;…………………………6分
③当![]() 时,由
时,由![]() 得
得![]() ,∴
,∴![]() 或
或![]() (舍去)
(舍去)
∴![]() 在
在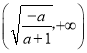 上单调递增,在
上单调递增,在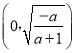 上单调递减;……………………8分
上单调递减;……………………8分
综上,当![]() 时,
时, ![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 在
在 单调递增,在
单调递增,在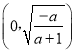 上单调递减.
上单调递减.
当![]() 时,
时, ![]() 在
在![]() 单调递减;
单调递减;
(3)由(2)知,当![]() 时,
时, 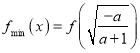 ,
,
即原不等式等价于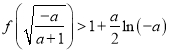 ,…………………………12分
,…………………………12分
即![]() ,整理得
,整理得![]() ,
,
∴![]() ,………………13分
,………………13分
又∵![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .……………………14分
.……………………14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
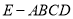 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.(1)求
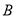 到平面
到平面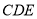 的距离
的距离(2)在线段
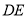 上是否存在一点
上是否存在一点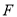 ,使
,使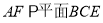 ?若存在,求出
?若存在,求出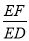 的值;若不存在,说明理由.
的值;若不存在,说明理由.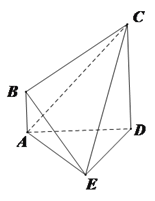
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知坐标平面上点
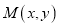 与两个定点
与两个定点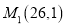 ,
, 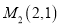 的距离之比等于5.
的距离之比等于5.(1)求点
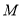 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为
 ,过点
,过点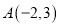 的直线
的直线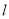 被
被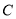 所截得的线段的长为 8,求直线
所截得的线段的长为 8,求直线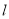 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=xlnx,g(x)=x3+ax2-x+2.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)对任意x∈(0,+∞),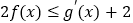 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求与圆心在直线
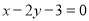 上,且过点A(2,-3),B(-2,-5)的圆C的方程.
上,且过点A(2,-3),B(-2,-5)的圆C的方程.(2)设
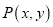 是圆C上的点,求
是圆C上的点,求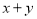 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=lg(ax﹣bx),且f(1)=lg2,f(2)=lg12
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)m为何值时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
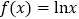 .
.(1)证明:
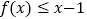 ;
;(2)若对任意
 ,不等式
,不等式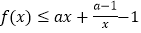 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
相关试题

