【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
语文成绩 | 60 | 70 | 74 | 90 | 94 | 110 |
历史成绩 | 58 | 63 | 75 | 79 | 81 | 88 |
(Ⅰ)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(Ⅱ)用表中数据画出散点图易发现历史成绩![]() 与语文成绩
与语文成绩![]() 具有较强的线性相关关系,求
具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).
参考公式:回归直线方程是![]() ,其中
,其中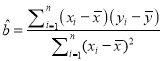 ,
, ![]()
参考答案:
【答案】(Ⅰ)24、16.(Ⅱ) ![]()
【解析】试题分析:
(1)将频率试作概率,按照表中所给数据计算优秀人数即可;
(2)利用计算公式分别求得![]() 的值即可求得回归直线方程.
的值即可求得回归直线方程.
试题解析:
(Ⅰ)由表中数据,语文成绩、历史成绩为优秀的频率分别为![]() ,
, ![]() ,
,
故该班语文、历史成绩优秀的人数分别为24、16.
(Ⅱ)由表中数据可得, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
所以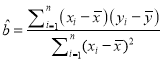
![]() ,
, ![]() ,
,
所以![]() 与
与![]() 的线性回归方程为
的线性回归方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=asin2x+bcos2x(ab≠0),有下列四个命题:其中正确命题的序号为(填上所有正确命题的序号)
①若a=1,b=﹣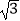 ,要得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移
,要得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移  个单位;
个单位;
②若a=1,b=﹣1,则函数y=f(x)的一个对称中心为( ,0);
,0);
③若y=f(x)的一条对称轴方程为x= ,则a=b;
,则a=b;
④若方程asin2x+bcos2x=m的正实数根从小到大依次构成一个等差数列,则这个等差数列的公差为π. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 且
且 ,若
,若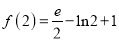 ,
,  在
在 处切线的斜率为
处切线的斜率为 .
.(1)求函数
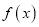 的解析式及其单调区间;
的解析式及其单调区间;(2)若实数
 满足
满足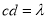 ,且
,且 对于任意
对于任意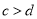 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间共有
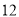 名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 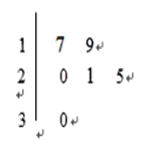
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间
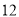 名工人中有几名优秀工人;
名工人中有几名优秀工人;(Ⅲ) 从该车间
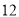 名工人中,任取2人,求恰有1名优秀工人的概率.
名工人中,任取2人,求恰有1名优秀工人的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】公元
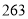 年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值
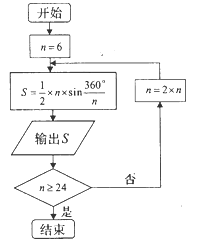
年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值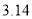 ,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中
,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中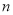 表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )
表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )(参考数据:
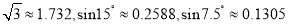 )
)
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
-
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了 1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日 期
1月10日
2月10日
3月10日
4月10日
5月10日
6月10日
昼夜温差x(°C)
10
11
13
12
8
6
就诊人数y(个)
22
25
29
26
16
12
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻两个月的概率;
(2)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程
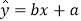 ;
; (3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考:用最小二乘法求线性回归方程系数公式
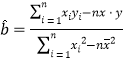 ,
,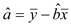 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了解学生在课外读物方面的支出情况,抽取了n名同学进行调查,结果显示这些同学的支出都在[10,50)(单位:元),其中支出在[30,50)(单位:元)的同学有67人,其频率分布直方图如图所示,则n的值为( )
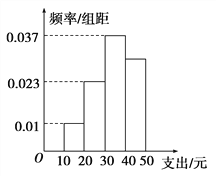
A. 100 B. 120 C. 130 D. 390
相关试题

