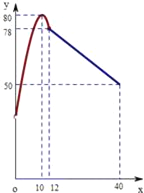
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.

参考答案:
【答案】(1)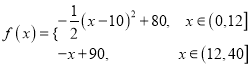 ;(2)老师在
;(2)老师在![]() 时段内安排核心内容,能使得学生学习效果最佳.
时段内安排核心内容,能使得学生学习效果最佳.
【解析】
试题(1)先根据顶点式设二次函数解析式,再代入点求开口,最后利用待定系数法求一次函数解析式,写成分段函数形式(2)由题意解不等式,先分段求解,再求并集
试题解析:解:(1)当x∈(0,12]时,
设f(x)=a(x﹣10)2+80
过点(12,78)代入得,![]()
则![]()
当x∈[12,40]时,
设y=kx+b,过点B(12,78)、C(40,50)
得![]() ,即y=﹣x+90
,即y=﹣x+90
则的函数关系式为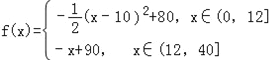
(2)由题意得,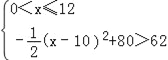 或
或![]()
得4<x≤12或12<x<28,
4<x<28
则老师就在x∈(4,28)时段内安排核心内容,能使得学生学习效果最佳.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
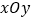 中,曲线
中,曲线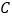 的参数方程为
的参数方程为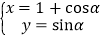 (
(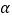 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,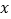 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线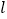 的极坐标方程为
的极坐标方程为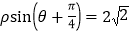 .
.(1)求曲线
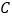 和直线
和直线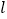 在该直角坐标系下的普通方程;
在该直角坐标系下的普通方程;(2)动点
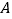 在曲线
在曲线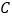 上,动点
上,动点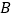 在直线
在直线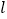 上,定点
上,定点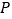 的坐标为
的坐标为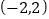 ,求
,求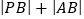 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
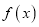 是定义域为
是定义域为 的奇函数,且当
的奇函数,且当 时,
时,  ,设
,设 “
“ ”.
”.(1)若
 为真,求实数
为真,求实数 的取值范围;
的取值范围;(2)设
 集合
集合 与集合
与集合 的交集为
的交集为 ,若
,若 为假,
为假,  为真,求实数
为真,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
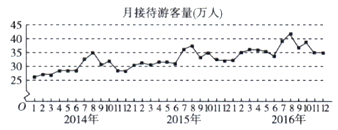
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
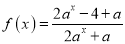 (
(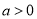 且
且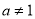 )是定义在
)是定义在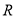 上的奇函数.
上的奇函数.(Ⅰ)求
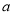 的值;
的值;(Ⅱ)求函数
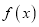 的值域;
的值域;(Ⅲ)当
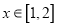 时,
时, 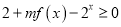 恒成立,求实数
恒成立,求实数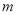 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成
 两组,每组100只,其中
两组,每组100只,其中 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液, 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记
 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于 ”,根据直方图得到
”,根据直方图得到 的估计值为
的估计值为 .
.(1)求乙离子残留百分比直方图中
 的值;
的值;(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
-
科目: 来源: 题型:
查看答案和解析>>【题目】对某市工薪阶层关于“楼市限购政策”的态度进行调查,随机抽查了
 人,他们月收入(单位:百元)的频数分布及对“楼市限购政策”赞成人数如下表:
人,他们月收入(单位:百元)的频数分布及对“楼市限购政策”赞成人数如下表:月收入(百元)






频数
5
10
15
10
5
5
赞成人数
4
8
12
5
2
1
(1))根据以上统计数据填写下面
 列联表,并回答是否有
列联表,并回答是否有 的把握认为月收入以
的把握认为月收入以 百元为分界点对“楼市限购政策”的态度有差异?
百元为分界点对“楼市限购政策”的态度有差异?月收入低于55百元人数
月收入不低于55百元人数
总计
赞成


不赞成
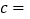

总计
(2)若从月收入在
 的被调查对象中随机选取
的被调查对象中随机选取 人进行调查,求至少有一人赞成“楼市限购政策”的概率.
人进行调查,求至少有一人赞成“楼市限购政策”的概率.(参考公式:
 ,其中
,其中 )
)参考值表:

0.050
0.010
0.001

3.841
6.635
10.828
相关试题

