【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 在该直角坐标系下的普通方程;
在该直角坐标系下的普通方程;
(2)动点![]() 在曲线
在曲线![]() 上,动点
上,动点![]() 在直线
在直线![]() 上,定点
上,定点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1) 曲线![]() 的普通方程为
的普通方程为![]() ;直线
;直线![]() 的方程是
的方程是![]() .
.
(2) ![]() .
.
【解析】
试题分析:(1)消去参数,根据三角函数的基本关系式,即可得到曲线![]() 的普通方程;利用极坐标与直角坐标的对应关系得到直线
的普通方程;利用极坐标与直角坐标的对应关系得到直线![]() 的普通方程;(2)求出点
的普通方程;(2)求出点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则
,则![]() 的最小为
的最小为![]() 到圆心的距离减去曲线
到圆心的距离减去曲线![]() 的半径.
的半径.
试题解析:(1)由曲线![]() 的参数方程
的参数方程![]() 可得
可得![]() ,
,
所以曲线![]() 的普通方程为
的普通方程为![]() .
.
由直线![]() 的极坐标方程:
的极坐标方程:![]() ,可得
,可得![]() ,即
,即![]() .
.
(2)设点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,有:
,有: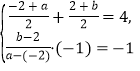 ,解得:
,解得:![]()
由(1)知,曲线![]() 为圆,圆心坐标为
为圆,圆心坐标为![]() ,故
,故
![]() .
.
当![]() 四点共线时,且
四点共线时,且![]() 在
在![]() 之间时,等号成立,所以
之间时,等号成立,所以![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)(2017·长春市二模)如图,在四棱锥
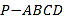 中,底面
中,底面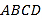 是菱形,
是菱形,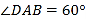 ,
,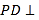 平面
平面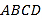 ,
,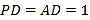 ,点
,点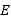 ,
,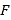 分别为
分别为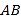 和
和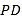 中点.
中点.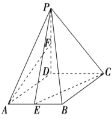
(1)求证:直线
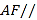 平面
平面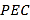 ;
;(2)求
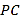 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线
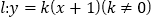 与椭圆
与椭圆 相交于
相交于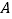 ,
,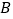 两个不同的点,与
两个不同的点,与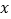 轴相交于点
轴相交于点 ,
,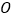 为坐标原点.
为坐标原点.(1)证明:
 ;
;(2)若
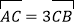 ,求
,求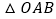 的面积取得最大值时椭圆的方程.
的面积取得最大值时椭圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
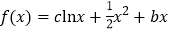
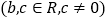 ,且
,且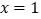 为
为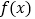 的极值点.
的极值点.(Ⅰ) 若
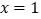 为
为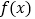 的极大值点,求
的极大值点,求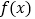 的单调区间(用
的单调区间(用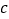 表示);
表示);(Ⅱ)若
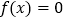 恰有1解,求实数
恰有1解,求实数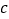 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
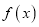 是定义域为
是定义域为 的奇函数,且当
的奇函数,且当 时,
时,  ,设
,设 “
“ ”.
”.(1)若
 为真,求实数
为真,求实数 的取值范围;
的取值范围;(2)设
 集合
集合 与集合
与集合 的交集为
的交集为 ,若
,若 为假,
为假,  为真,求实数
为真,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
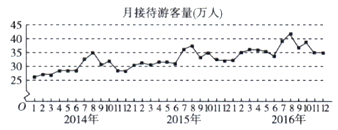
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.

相关试题

