【题目】已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,若双曲线上存在点
,若双曲线上存在点![]() ,使
,使![]() ,则该双曲线的离心率
,则该双曲线的离心率![]() 范围为( )
范围为( )
A. (1,1![]() ) B. (1,1
) B. (1,1![]() ) C. (1,1
) C. (1,1![]() ] D. (1,1
] D. (1,1![]() ]
]
参考答案:
【答案】A
【解析】由题意,点![]() 不是双曲线的顶点,否则
不是双曲线的顶点,否则![]() 无意义,在
无意义,在![]() 中,由正弦定理得
中,由正弦定理得![]() ,又
,又![]() ,即
,即![]() ,
, ![]() 在双曲线的右支上,由双曲线的定义,得
在双曲线的右支上,由双曲线的定义,得![]() ,即
,即![]() ,由双曲线的几何性质,知
,由双曲线的几何性质,知![]() ,即
,即![]() ,
, ![]() ,解得
,解得![]() ,又
,又![]() ,所以双曲线离心率的范围是
,所以双曲线离心率的范围是![]() ,故选A.
,故选A.
【方法点晴】本题主要考查正弦定理以及利用双曲线的简单性质求双曲线的离心率范围,属于难题.求解与双曲线性质有关的问题时要结合图形进行分析,既使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.求离心率问题应先将 ![]() 用有关的一些量表示出来,再利用其中的一些关系构造出关于
用有关的一些量表示出来,再利用其中的一些关系构造出关于![]() 的不等式,从而求出
的不等式,从而求出![]() 的范围.焦半径构造出关于
的范围.焦半径构造出关于![]() 的不等式,最后解出
的不等式,最后解出![]() 的范围.
的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为评估设备
 生产某种零件的性能,从设备
生产某种零件的性能,从设备 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:直径/

58
59
61
62
63
64
65
66
67
68
69
70
71
73
合计
件数
1
1
3
5
6
19
33
18
4
4
2
1
2
1
100
经计算,样本的平均值
 ,标准差
,标准差 ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为
 ,并根据以下不等式进行评判(
,并根据以下不等式进行评判( 表示相应事件的概率);
表示相应事件的概率);①
 ;
;②
 ;
;③

评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备
 的性能等级.
的性能等级.(2)将直径小于等于
 或直径大于
或直径大于 的零件认为是次品.
的零件认为是次品.①从设备
 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数 的数学期望
的数学期望 ;
;②从样本中随意抽取2件零件,计算其中次品个数
 的数学期望
的数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
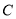 :
: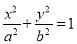
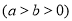 上的任一点到焦点的距离最大值为3,离心率为
上的任一点到焦点的距离最大值为3,离心率为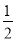 ,
,(1)求椭圆
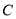 的标准方程;
的标准方程;(2)若
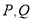 为曲线
为曲线 上两点,
上两点, 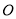 为坐标原点,直线
为坐标原点,直线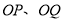 的斜率分别为
的斜率分别为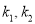 ,且
,且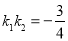 ,求直线
,求直线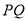 被圆
被圆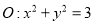 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线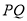 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
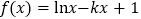 .
.(1)求函数
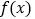 的单调区间;
的单调区间;(2)若
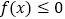 恒成立,试确定实数
恒成立,试确定实数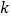 的取值范围;
的取值范围;(3)证明:
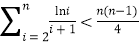
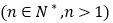 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)五边形
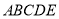 中,
中, 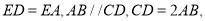
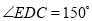 ,将
,将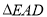 沿
沿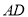 折到
折到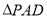 的位置,得到四棱锥
的位置,得到四棱锥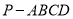 ,如图(2),点
,如图(2),点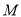 为线段
为线段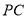 的中点,且
的中点,且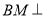 平面
平面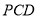 .
.(1)求证:平面
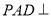 平面
平面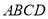 ;
;(2)若直线
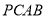 与所成角的正切值为
与所成角的正切值为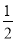 ,求直线
,求直线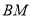 与平面
与平面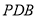 所成角的正弦值.
所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用,勘探初期数据资料见如表:

(参考公式和计算结果:
 ,
,  ,
,  ,
,  )
)(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为
 ,求
,求 的值,并估计
的值,并估计 的预报值.
的预报值.(2)现准备勘探新井
 ,若通过1,3,5,7号并计算出的
,若通过1,3,5,7号并计算出的 ,
,  的值(
的值( ,
,  精确到0.01)相比于(1)中的
精确到0.01)相比于(1)中的 ,
,  ,值之差不超过10%,则使用位置最接近的已有旧井
,值之差不超过10%,则使用位置最接近的已有旧井 ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?(3)设出油量与勘探深度的比值
 不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数
不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
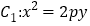 的焦点在抛物线
的焦点在抛物线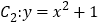 上,点
上,点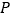 是抛物线
是抛物线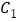 上的动点.
上的动点.(1)求抛物线
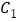 的方程及其准线方程;
的方程及其准线方程;(2)过点
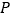 作抛物线
作抛物线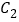 的两条切线,
的两条切线, 、
、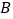 分别为两个切点,求
分别为两个切点,求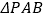 面积的最小值.
面积的最小值.
相关试题

