【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的概率);
表示相应事件的概率);
①![]() ;
;
②![]() ;
;
③![]()
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
①从设备![]() 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
②从样本中随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.
参考答案:
【答案】(I)丙;(II)(ⅰ)![]() ;(ⅱ)
;(ⅱ)![]() .
.
【解析】试题分析:(1)运用相关系数进行判别推理;(2)运用贝努力分布的几何分布求解期望.
试题解析:
(1)![]()
![]()
![]()
因为设备![]() 的数据仅满足一个不等式,故其性能等级为丙;
的数据仅满足一个不等式,故其性能等级为丙;
(2)易知样本中次品共6件,可估计设备![]() 生产零件的次品率为0.06.
生产零件的次品率为0.06.
(ⅰ)由题意可知![]() ~
~![]() ,于是
,于是![]() ,
,
(ⅱ)由题意可知![]() 的分布列为
的分布列为

故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
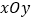 中,曲线
中,曲线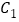 的参数方程为
的参数方程为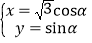 (其中
(其中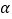 为参数),曲线
为参数),曲线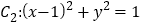 ,以坐标原点
,以坐标原点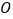 为极点,以
为极点,以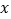 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.(1)求曲线
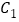 的普通方程和曲线
的普通方程和曲线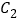 的极坐标方程;
的极坐标方程;(2)若射线
 与曲线
与曲线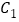 ,
,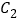 分别交于
分别交于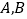 两点,求
两点,求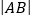 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的,祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都为
 ),其中:三棱锥的底面是正三角形(边长为
),其中:三棱锥的底面是正三角形(边长为 ),四棱锥的底面是有一个角为
),四棱锥的底面是有一个角为 的菱形(边长为
的菱形(边长为 ),圆锥的体积为
),圆锥的体积为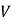 ,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )A.
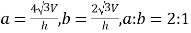 B.
B. 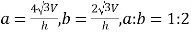
C.
 D.
D. 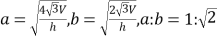
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
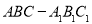 中,已知
中,已知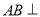 侧面
侧面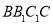 ,
,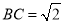 ,
,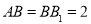 ,
,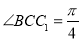 ,点
,点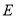 在棱
在棱 上.
上.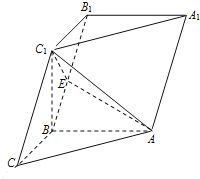
(Ⅰ)求证:
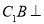 平面
平面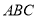 ;
;(Ⅱ)试确定点
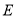 的位置,使得二面角
的位置,使得二面角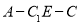 的余弦值为
的余弦值为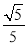 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
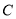 :
: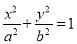
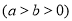 上的任一点到焦点的距离最大值为3,离心率为
上的任一点到焦点的距离最大值为3,离心率为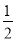 ,
,(1)求椭圆
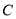 的标准方程;
的标准方程;(2)若
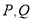 为曲线
为曲线 上两点,
上两点, 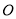 为坐标原点,直线
为坐标原点,直线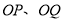 的斜率分别为
的斜率分别为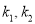 ,且
,且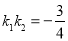 ,求直线
,求直线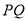 被圆
被圆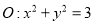 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线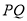 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
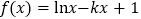 .
.(1)求函数
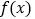 的单调区间;
的单调区间;(2)若
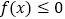 恒成立,试确定实数
恒成立,试确定实数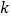 的取值范围;
的取值范围;(3)证明:
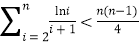
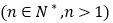 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
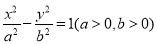 的左,右焦点分别为
的左,右焦点分别为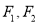 ,若双曲线上存在点
,若双曲线上存在点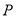 ,使
,使 ,则该双曲线的离心率
,则该双曲线的离心率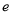 范围为( )
范围为( )A. (1,1
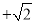 ) B. (1,1
) B. (1,1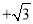 ) C. (1,1
) C. (1,1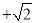 ] D. (1,1
] D. (1,1 ]
]
相关试题

