【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上的最大值是
上的最大值是![]() ,求
,求![]() 的值;
的值;
(3)记![]() ,当
,当![]() 时,若对任意
时,若对任意![]() ,总有
,总有![]() 成立,试求
成立,试求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)增区间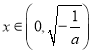 ;减区间
;减区间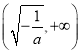 ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数的知识求解;(2)借助题设运用分类整合思想探求;(3)借助题设构造函数,运用导数的有关知识分析探求.
试题解析:
(1)![]() 的定义域是
的定义域是![]() .
.![]() .当
.当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是增函数; 当
上是增函数; 当![]() 时,令
时,令![]() ,则
,则![]() (舍去); 当
(舍去); 当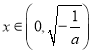 时,
时,![]() ,故
,故![]() 在
在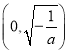 上是增函数;当
上是增函数;当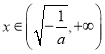 时,
时,![]() ,故
,故![]() 在
在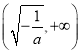 上是减函数.
上是减函数.
(2)①当![]() 时,
时,![]() 在
在![]() 上是增函数; 故在
上是增函数; 故在![]() 上的最大值是
上的最大值是 ![]() ,显然不合题意. ②若
,显然不合题意. ②若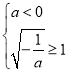 , 即
, 即![]() 时,
时, 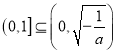 ,则
,则![]() 在
在![]() 上是增函数,故在
上是增函数,故在![]() 上的最大值是
上的最大值是 ![]() ,不合题意,舍去.
,不合题意,舍去.
③ 若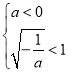 , 即
, 即![]() 时,
时,![]() 在
在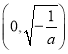 上是增函数 ,在
上是增函数 ,在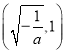 上是减函数,故在
上是减函数,故在![]() 上的最大值是
上的最大值是 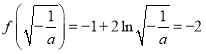 , 解得
, 解得![]() ,符合. 综合①、②、③得:
,符合. 综合①、②、③得: ![]() .
.
(3)![]() , 则
, 则![]() ,当
,当![]() 时,
时,![]() ,故
,故![]() 时,当
时,当![]() 在
在![]() 上是减函数,不妨设
上是减函数,不妨设![]() ,则
,则![]() ,故
,故![]() 等价于
等价于![]() ,即
,即![]() ,记
,记
![]() ,从而
,从而![]() 在
在![]() 上为减函数,由
上为减函数,由![]() 得:
得:
![]() ,故
,故![]() 恒成立,
恒成立,![]() ,又
,又
![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() .故当
.故当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】亳州某商场举行购物抽奖活动,规定每位顾客从装有编号为0,1,2,3四个相同小求的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码相加之和等于6,则中一等奖;等于5中二等奖;等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求不中奖的概率.
-
科目: 来源: 题型:
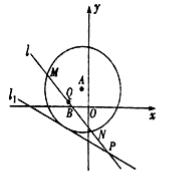
查看答案和解析>>【题目】如图所示,已知圆
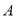 的圆心在直线
的圆心在直线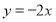 上,且该圆存在两点关于直线
上,且该圆存在两点关于直线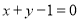 对称,又圆
对称,又圆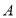 与直线
与直线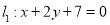 相切,过点
相切,过点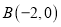 的动直线
的动直线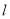 与圆
与圆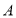 相交于
相交于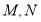 两点,
两点,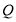 是
是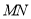 的中点,直线
的中点,直线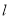 与
与 相交于点
相交于点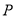 .
.
(1)求圆
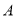 的方程;
的方程;(2)当
 时,求直线
时,求直线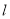 的方程;
的方程;(3)
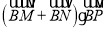 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
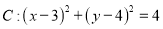 ,直线
,直线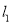 经过点A (1,0).
经过点A (1,0).(1)若直线
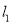 与圆C相切,求直线
与圆C相切,求直线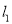 的方程;
的方程; (2)若直线
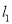 与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线
与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线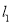 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是公差为
是公差为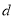 的等差数列,
的等差数列, 是公比为
是公比为 的等比数列. 记
的等比数列. 记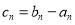 .
.(1)求证: 数列
 为等比数列;
为等比数列;(2)已知数列
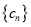 的前
的前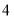 项分别为
项分别为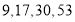 .
.①求数列
 和
和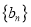 的通项公式;
的通项公式;②是否存在元素均为正整数的集合
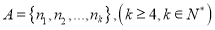 ,使得数列
,使得数列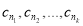 等差数列?证明你的结论.
等差数列?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
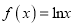 ,
, 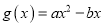 (
(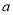 、
、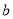 为常数).
为常数). (Ⅰ)求函数
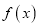 在点
在点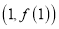 处的切线方程;
处的切线方程;(Ⅱ)当函数
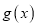 在
在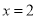 处取得极值
处取得极值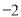 ,求函数
,求函数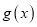 的解析式;
的解析式;(Ⅲ)当
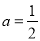 时,设
时,设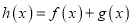 ,若函数
,若函数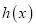 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数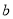 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
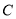 :
: 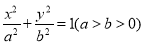 的离心率
的离心率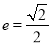 ,左、右焦点分别为
,左、右焦点分别为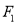 ,
, 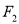 ,点
,点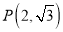 满足:
满足: 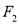 在线段
在线段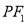 的中垂线上.
的中垂线上.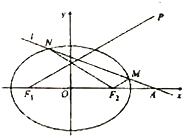
(Ⅰ)求椭圆
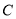 的方程;
的方程;(Ⅱ)若斜率为
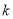 (
( )的直线
)的直线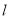 与
与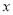 轴、椭圆
轴、椭圆 顺次相交于点
顺次相交于点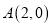 、
、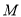 、
、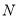 ,且
,且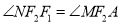 ,求
,求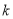 的取值范围.
的取值范围.
相关试题

