【题目】已知函数![]() ,
, ![]() (
(![]() 、
、![]() 为常数).
为常数).
(Ⅰ)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当函数![]() 在
在![]() 处取得极值
处取得极值![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(Ⅲ)当![]() 时,设
时,设![]() ,若函数
,若函数![]() 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)先根据导数几何意义得![]() ,再利用点斜式求切线方程,(2)由极值定义得
,再利用点斜式求切线方程,(2)由极值定义得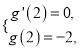 解方程组得
解方程组得![]() ,
, ![]() .最后需验证极值条件.(3)由题意得存在
.最后需验证极值条件.(3)由题意得存在![]() 使
使![]() ,即存在
,即存在![]() 使
使![]() ,利用变量分离得
,利用变量分离得![]() 的最小值,即
的最小值,即![]() .
.
试题解析:(Ⅰ)由![]() (
(![]() ),可得
),可得![]() (
(![]() ),
),
∴![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() ,即
,即![]() ,所求切线方程为
,所求切线方程为![]() .
.
(Ⅱ)∵又![]() 可得
可得![]() ,且
,且![]() 在
在![]() 处取得极值
处取得极值![]() .
.
∴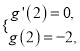 可得
可得![]() 解得
解得![]() ,
, ![]() .
.
所求![]() (
(![]() ).
).
(Ⅲ)∵![]() ,
, ![]() (
(![]() ).
).
依题存在![]() 使
使![]() ,∴即存在
,∴即存在![]() 使
使![]() ,
,
不等式![]() 等价于
等价于![]() (*)
(*)
令![]() (
(![]() ),∵
),∵![]() .
.
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,故
上递增,故![]() ,
,
∵存在![]() ,不等式(*)成立,∴
,不等式(*)成立,∴![]() .所求
.所求![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
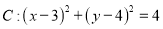 ,直线
,直线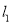 经过点A (1,0).
经过点A (1,0).(1)若直线
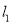 与圆C相切,求直线
与圆C相切,求直线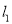 的方程;
的方程; (2)若直线
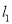 与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线
与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线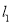 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求
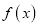 的单调区间;
的单调区间;(2)若
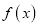 在
在 上的最大值是
上的最大值是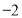 ,求
,求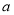 的值;
的值;(3)记
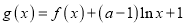 ,当
,当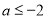 时,若对任意
时,若对任意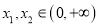 ,总有
,总有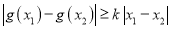 成立,试求
成立,试求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是公差为
是公差为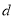 的等差数列,
的等差数列, 是公比为
是公比为 的等比数列. 记
的等比数列. 记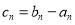 .
.(1)求证: 数列
 为等比数列;
为等比数列;(2)已知数列
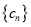 的前
的前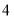 项分别为
项分别为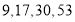 .
.①求数列
 和
和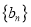 的通项公式;
的通项公式;②是否存在元素均为正整数的集合
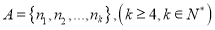 ,使得数列
,使得数列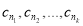 等差数列?证明你的结论.
等差数列?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
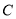 :
: 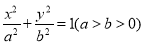 的离心率
的离心率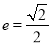 ,左、右焦点分别为
,左、右焦点分别为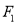 ,
, 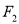 ,点
,点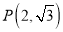 满足:
满足: 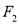 在线段
在线段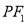 的中垂线上.
的中垂线上.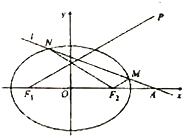
(Ⅰ)求椭圆
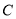 的方程;
的方程;(Ⅱ)若斜率为
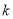 (
( )的直线
)的直线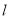 与
与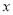 轴、椭圆
轴、椭圆 顺次相交于点
顺次相交于点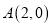 、
、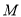 、
、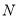 ,且
,且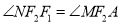 ,求
,求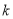 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,太湖一个角形湖湾
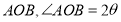 ( 常数
( 常数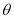 为锐角). 拟用长度为
为锐角). 拟用长度为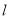 (
(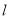 为常数)的围网围成一个养殖区,有以下两种方案可供选择:
为常数)的围网围成一个养殖区,有以下两种方案可供选择:方案一 如图1,围成扇形养殖区
 ,其中
,其中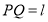 ;
;方案二 如图2,围成三角形养殖区
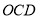 ,其中
,其中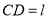 ;
;
(1)求方案一中养殖区的面积
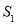 ;
;(2)求方案二中养殖区的最大面积
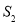 ;
;(3)为使养殖区的面积最大,应选择何种方案?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂第一季度某产品月生产量依次为10万件,12万件,13万件,为了预测以后每个月的产量,以这3个月的产量为依据,用一个函数模拟该产品的月产量
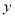 (单位:万件)与月份
(单位:万件)与月份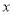 的关系. 模拟函数
的关系. 模拟函数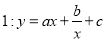 ;模拟函数
;模拟函数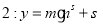 .
.(1)已知4月份的产量为万件,问选用哪个函数作为模拟函数好?
(2)受工厂设备的影响,全年的每月产量都不超过15万件,请选用合适的模拟函数预测6月份的产量.
相关试题

