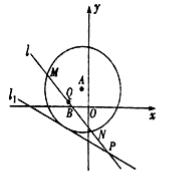
【题目】如图所示,已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且该圆存在两点关于直线
上,且该圆存在两点关于直线![]() 对称,又圆
对称,又圆![]() 与直线
与直线![]() 相切,过点
相切,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)![]() 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)是,
;(3)是,![]() .
.
【解析】
试题分析:(1)借助题设条件构建方程组求解;(2)借助题设建立方程组求解;(3)运用向量的坐标形式的运算推证求解.
试题解析:
(1)由圆存在两点关于直线![]() 对称知圆心
对称知圆心![]() 在直线
在直线![]() 上,
上,
由![]() 得
得![]() .
.
设圆![]() 的半径为
的半径为![]() ,因为圆
,因为圆![]() 与直线
与直线![]() 相切,
相切,
所以![]() .
.
所以圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 与
与![]() 轴垂直时,易知
轴垂直时,易知![]() 符合题意..
符合题意..
当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
即![]() 连接
连接![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,
,
由![]() ,得
,得![]()
∴直线![]() 的方程为
的方程为![]() .
.
∴所求直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(3)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
当直线![]() 与
与![]() 轴垂直时,得
轴垂直时,得![]() ,则
,则![]() ,又
,又![]() ,
,
∴![]()
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
∴![]()
综上所述,![]() 是定值,且为-10.
是定值,且为-10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
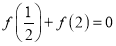 ,求
,求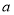 的值;
的值;(2)若存在
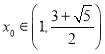 ,使函数
,使函数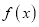 的图像在点
的图像在点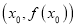 和点
和点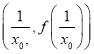 处的切线互相垂直,求
处的切线互相垂直,求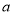 的取值范围;
的取值范围;(3)若函数
 在区间
在区间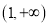 上有两个极值点,则是否存在实数
上有两个极值点,则是否存在实数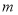 ,使
,使 对任意的
对任意的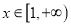 恒成立?若存在,求出
恒成立?若存在,求出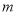 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一个八面体各棱长均为1,四边形ABCD为正方形,则下列命题中不正确的是
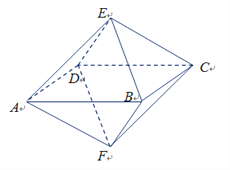
A. 不平行的两条棱所在直线所成的角为
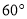 或
或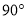 B. 四边形AECF为正方形
B. 四边形AECF为正方形C. 点A到平面BCE的距离为
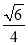 D. 该八面体的顶点在同一个球面上
D. 该八面体的顶点在同一个球面上 -
科目: 来源: 题型:
查看答案和解析>>【题目】亳州某商场举行购物抽奖活动,规定每位顾客从装有编号为0,1,2,3四个相同小求的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码相加之和等于6,则中一等奖;等于5中二等奖;等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求不中奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
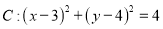 ,直线
,直线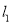 经过点A (1,0).
经过点A (1,0).(1)若直线
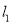 与圆C相切,求直线
与圆C相切,求直线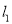 的方程;
的方程; (2)若直线
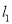 与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线
与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线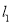 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求
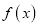 的单调区间;
的单调区间;(2)若
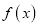 在
在 上的最大值是
上的最大值是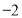 ,求
,求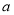 的值;
的值;(3)记
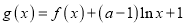 ,当
,当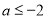 时,若对任意
时,若对任意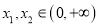 ,总有
,总有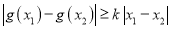 成立,试求
成立,试求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是公差为
是公差为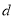 的等差数列,
的等差数列, 是公比为
是公比为 的等比数列. 记
的等比数列. 记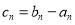 .
.(1)求证: 数列
 为等比数列;
为等比数列;(2)已知数列
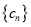 的前
的前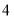 项分别为
项分别为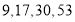 .
.①求数列
 和
和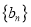 的通项公式;
的通项公式;②是否存在元素均为正整数的集合
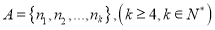 ,使得数列
,使得数列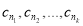 等差数列?证明你的结论.
等差数列?证明你的结论.
相关试题

