【题目】设![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列. 记
的等比数列. 记![]() .
.
(1)求证: 数列![]() 为等比数列;
为等比数列;
(2)已知数列![]() 的前
的前![]() 项分别为
项分别为![]() .
.
①求数列![]() 和
和![]() 的通项公式;
的通项公式;
②是否存在元素均为正整数的集合![]() ,使得数列
,使得数列![]() 等差数列?证明你的结论.
等差数列?证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)①![]() ;②不存在满足题意的集合
;②不存在满足题意的集合![]() .
.
【解析】
试题分析:(1)借助题设条件运用等比数列的定义推证;(2)借助题设运用等差数列及分析推证法探求.
试题解析:
(1)证明:
依题意,![]() ,
,
从而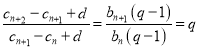 , 又
, 又![]()
![]() ,所以
,所以![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列 .
的等比数列 .
(2)① 由(1)得,等比数列![]() 的前
的前![]() 项为
项为![]() , 则
, 则![]() ,解得
,解得![]() , 从而
, 从而![]() , 且
, 且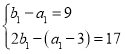 , 解得
, 解得![]() ,所以
,所以![]() .
.
②假设存在满足题意的集合![]() ,不妨设
,不妨设![]() , 且
, 且![]() 等差数列, 则
等差数列, 则![]() , 因为
, 因为![]() , 所以
, 所以![]() ① 若
① 若![]() , 则
, 则![]() ,结合①得,
,结合①得, ![]() , 则
, 则![]() , 化简得,
, 化简得,
![]() , ② 因为
, ② 因为![]() , 不难知
, 不难知![]() ,这与②矛盾,所以只能
,这与②矛盾,所以只能![]() ,同理
,同理![]() , 所以
, 所以![]() 为数列
为数列![]() 的连续三项,从而
的连续三项,从而![]() ,即
,即
![]() ,又
,又![]() .故
.故![]() ,又
,又![]() ,故
,故![]() , 这与
, 这与![]() 矛盾,所以假设不成立,从而不存在满足题意的集合
矛盾,所以假设不成立,从而不存在满足题意的集合![]() .
.
-
科目: 来源: 题型:
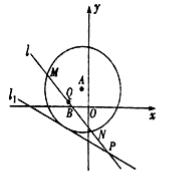
查看答案和解析>>【题目】如图所示,已知圆
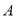 的圆心在直线
的圆心在直线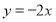 上,且该圆存在两点关于直线
上,且该圆存在两点关于直线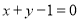 对称,又圆
对称,又圆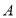 与直线
与直线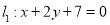 相切,过点
相切,过点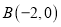 的动直线
的动直线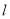 与圆
与圆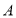 相交于
相交于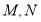 两点,
两点,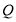 是
是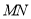 的中点,直线
的中点,直线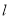 与
与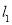 相交于点
相交于点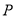 .
.
(1)求圆
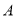 的方程;
的方程;(2)当
 时,求直线
时,求直线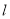 的方程;
的方程;(3)
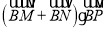 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
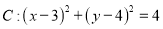 ,直线
,直线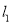 经过点A (1,0).
经过点A (1,0).(1)若直线
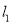 与圆C相切,求直线
与圆C相切,求直线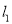 的方程;
的方程; (2)若直线
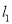 与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线
与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线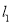 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求
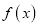 的单调区间;
的单调区间;(2)若
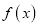 在
在 上的最大值是
上的最大值是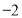 ,求
,求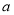 的值;
的值;(3)记
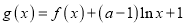 ,当
,当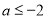 时,若对任意
时,若对任意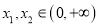 ,总有
,总有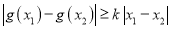 成立,试求
成立,试求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
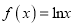 ,
, 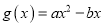 (
(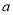 、
、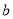 为常数).
为常数). (Ⅰ)求函数
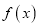 在点
在点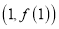 处的切线方程;
处的切线方程;(Ⅱ)当函数
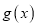 在
在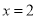 处取得极值
处取得极值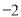 ,求函数
,求函数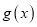 的解析式;
的解析式;(Ⅲ)当
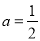 时,设
时,设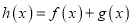 ,若函数
,若函数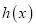 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数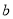 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
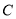 :
: 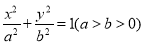 的离心率
的离心率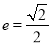 ,左、右焦点分别为
,左、右焦点分别为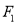 ,
, 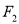 ,点
,点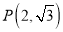 满足:
满足: 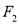 在线段
在线段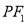 的中垂线上.
的中垂线上.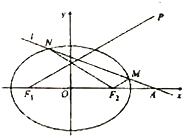
(Ⅰ)求椭圆
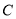 的方程;
的方程;(Ⅱ)若斜率为
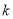 (
( )的直线
)的直线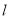 与
与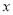 轴、椭圆
轴、椭圆 顺次相交于点
顺次相交于点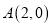 、
、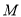 、
、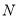 ,且
,且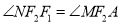 ,求
,求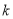 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,太湖一个角形湖湾
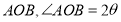 ( 常数
( 常数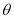 为锐角). 拟用长度为
为锐角). 拟用长度为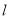 (
(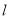 为常数)的围网围成一个养殖区,有以下两种方案可供选择:
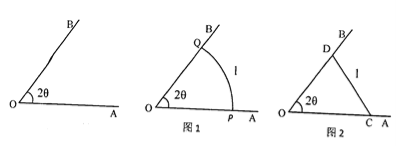
为常数)的围网围成一个养殖区,有以下两种方案可供选择:方案一 如图1,围成扇形养殖区
 ,其中
,其中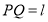 ;
;方案二 如图2,围成三角形养殖区
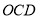 ,其中
,其中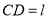 ;
;
(1)求方案一中养殖区的面积
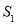 ;
;(2)求方案二中养殖区的最大面积
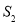 ;
;(3)为使养殖区的面积最大,应选择何种方案?并说明理由.
相关试题

