【题目】已知函数![]() 在区间
在区间![]() 上有最大值3和最小值
上有最大值3和最小值![]() .
.
(1)求实数![]() 的值;
的值;
(2)设![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】试题分析:(1)根据二次函数的性质求出![]() 的单调区间,求出函数的最大值和最小值,得到关于
的单调区间,求出函数的最大值和最小值,得到关于![]() 的方程组,解出即可;(2)问题转化为
的方程组,解出即可;(2)问题转化为![]() ,令
,令![]() ,根据函数的单调性求出
,根据函数的单调性求出![]() 的最小值,求出
的最小值,求出![]() 的范围即.
的范围即.
试题解析:(1)∵![]() 的对称轴是
的对称轴是![]() ,又∵
,又∵![]() .
.
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
∴当![]() 时,
时, ![]() 取最小值
取最小值![]() ,当
,当![]() 时,
时, ![]() 取最大值3;
取最大值3;
即![]() ,解得
,解得![]() .
.
(2)∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上是增函数,
上是增函数,
故![]() ,
,
∴![]() 在
在![]() 上恒成立时,
上恒成立时, ![]() .
.
【方法点晴】本题主要考查二次函数的最值以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.本题是利用方法 ① 求得
恒成立;④ 讨论参数.本题是利用方法 ① 求得![]() 的范围的.
的范围的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(A)在直角坐标系
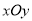 中,以坐标原点为极点,
中,以坐标原点为极点, 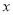 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线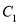 的参数方程为
的参数方程为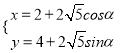 (
(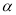 为参数),
为参数), 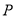 是曲线
是曲线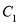 上的动点,
上的动点, 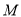 为线段
为线段 的中点,设点
的中点,设点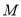 的轨迹为曲线
的轨迹为曲线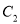 .
.(1)求
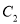 的坐标方程;
的坐标方程;(2)若射线
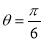 与曲线
与曲线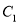 异于极点的交点为
异于极点的交点为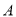 ,与曲线
,与曲线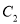 异于极点的交点为
异于极点的交点为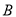 ,求
,求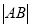 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
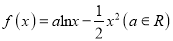 .
.(1)求
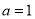 时,求
时,求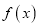 的单调区间;
的单调区间;(2)讨论
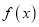 在定义域上的零点个数.
在定义域上的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 且
且 ,若
,若 ,
,  在
在 处切线的斜率为
处切线的斜率为 .
.(1)求函数
 的解析式及其单调区间;
的解析式及其单调区间;(2)若实数
 满足
满足 ,且
,且 对于任意
对于任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前
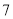 次考试的数学成绩
次考试的数学成绩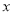 、物理成绩进行分析.下面是该生
、物理成绩进行分析.下面是该生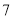 次考试的成绩.
次考试的成绩.数学
108
103
137
112
128
120
132
物理
74
71
88
76
84
81
86
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的说明;
(Ⅱ)已知该生的物理成绩
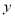 与数学成绩是线性相关的,求物理成绩
与数学成绩是线性相关的,求物理成绩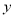 与数学成绩的回归直线方程
与数学成绩的回归直线方程(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附:
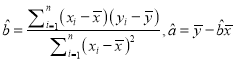 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四个命题:
①在回归分析中,
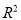 可以用来刻画回归效果,
可以用来刻画回归效果, 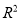 的值越大,模型的拟合效果越好;
的值越大,模型的拟合效果越好;②在独立性检验中,随机变量
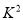 的值越大,说明两个分类变量有关系的可能性越大;
的值越大,说明两个分类变量有关系的可能性越大;③在回归方程
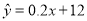 中,当解释变量
中,当解释变量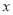 每增加1个单位时,预报变量
每增加1个单位时,预报变量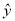 平均增加1个单位;
平均增加1个单位;④两个随机变量相关性越弱,则相关系数的绝对值越接近于1;
其中真命题是:
A. ①④ B. ②④ C. ①② D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”国际合作高峰论坛圆满落幕了,相关话题在网络上引起了网友们的高度关注,为此,21财经APP联合UC推出“一带一路”大数据微报告,在全国抽取的70千万网民中(其中
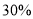 为高学历)有20千万人对此关注(其中
为高学历)有20千万人对此关注(其中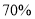 为高学历).
为高学历).(1)根据以上统计数据填下面
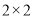 列联表;
列联表;(2)根据列联表,用独立性检验的方法分析,能否有
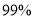 的把握认为“一带一路”的关注度与学历有关系?
的把握认为“一带一路”的关注度与学历有关系?高学历(千万人)
不是高学历(千万人)
合计
关注
不关注
合计
参考公式:
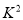 统计量的表达式是
统计量的表达式是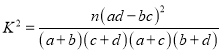 ,
, 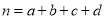
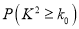

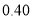
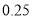
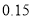

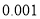

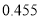
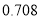
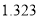
相关试题

