【题目】已知函数f(x)=cos2x﹣sinxcosx
(1)求f(x)的最小正周期;
(2)求函数f(x)的单调递增区间;
(3)求f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
参考答案:
【答案】
(1)解:f(x)=cos2x﹣sinxcosx
= ![]()
= ![]()
= ![]()
所以f(x)的最小正周期 ![]()
(2)解:令2kπ+ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,解得:kπ+
,k∈Z,解得:kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
可得函数f(x)的单调递增区间为:[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
(3)解:由 ![]() ,得
,得 ![]() ,
,
所以 ![]() ,
,
所以当 ![]() ,即x=0时,
,即x=0时, ![]() ;
;
当 ![]() ,即
,即 ![]() 时,
时, ![]()
【解析】(1)利用三角函数恒等变换的应用化简函数解析式可得f(x)= ![]() ,利用周期公式即可得解f(x)的最小正周期;(2)令2kπ+
,利用周期公式即可得解f(x)的最小正周期;(2)令2kπ+ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,即可求得函数f(x)的单调递增区间.(3)由
,k∈Z,即可求得函数f(x)的单调递增区间.(3)由 ![]() ,得
,得 ![]() ,进而可得
,进而可得 ![]() ,利用正弦函数的图象和性质即可得解.
,利用正弦函数的图象和性质即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
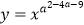 是偶函数,且在(0,+∞)是减函数,则整数a的值是 .
是偶函数,且在(0,+∞)是减函数,则整数a的值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面是边长为
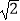 的正方形,AA1=3,点F在棱B1B上运动.
的正方形,AA1=3,点F在棱B1B上运动. 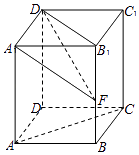
(1)若三棱锥B1﹣A1D1F的体积为 时,求异面直线AD与D1F所成的角
时,求异面直线AD与D1F所成的角
(2)求异面直线AC与D1F所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,定义在[﹣1,5]上的函数f(x)由一段线段和抛物线的一部分组成. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)指出函数f(x)的自变量x在什么范围内取值时,函数值大于0,小于0或等于0(不需说理由).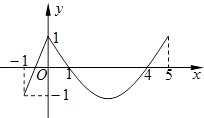
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 是直线
是直线 与函数
与函数 图像的两个相邻的交点,且
图像的两个相邻的交点,且 .
.(1)求
 的值和函数
的值和函数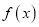 的单调增区间;
的单调增区间; (2)将函数
 的图象上各点的横坐标伸长为原来的
的图象上各点的横坐标伸长为原来的 倍(纵坐标不变),再将得到的图象向左平移
倍(纵坐标不变),再将得到的图象向左平移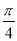 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 的对称轴方程.
的对称轴方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a为实数,函数f(x)=2x2+(x﹣a)|x﹣a|.
(1)若f(0)≥1,求a的取值范围;
(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥1的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】若Ai(i=1,2,3,…,n)是△AOB所在平面内的点,且
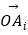
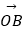 =
= 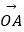
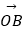 ,给出下列说法:
,给出下列说法:
·(1)|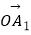 |=|
|=| 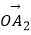 |=|
|=| 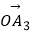 |=…=|
|=…=| 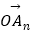 |
|
·(2)|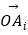 |的最小值一定是|
|的最小值一定是| 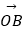 |
|
·(3)点A和点Ai一定共线
·(4)向量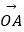 及
及 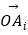 在向量
在向量 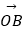 方向上的投影必定相等
方向上的投影必定相等
其中正确的个数是( )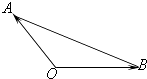
A.1个
B.2个
C.3个
D.4个
相关试题

