【题目】如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC. 
(Ⅰ)求BD的长;
(Ⅱ)求sin∠CBD的值.
参考答案:
【答案】解:(Ⅰ)因为∠ABC=90°,AB=4,BC=3, 所以cosC= ![]() ,sinC=
,sinC= ![]() ,AC=5,
,AC=5,
又因为AD=4DC,所以AD=4,DC=1.
在△BCD中,由余弦定理,
得BD2=BC2+CD2﹣2BCCDcosC
=32+12﹣2× ![]() =
= ![]() ,
,
所以 ![]() .
.
(Ⅱ)在△BCD中,由正弦定理,得 ![]() ,
,
所以 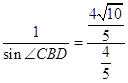 ,
,
所以 sin∠CBD= ![]()
【解析】(Ⅰ)由已知可求cosC,sinC,AC,又AD=4DC,可求AD,DC,从而由余弦定理BD2=BC2+CD2﹣2BCCDcosC即可求BD的值.(Ⅱ)在△BCD中,由正弦定理即可求得sin∠CBD的值.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
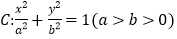 的短轴长为
的短轴长为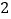 ,椭圆
,椭圆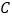 上任意一点到右焦点
上任意一点到右焦点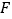 距 离的最大值为
距 离的最大值为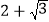 .
.(Ⅰ)求椭圆
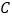 的标准方程;
的标准方程;(Ⅱ)过点
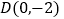 作直线
作直线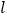 与曲线
与曲线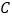 交于
交于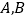 两点,点
两点,点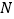 满足
满足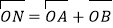 (
(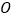 为坐标原点),求四边形
为坐标原点),求四边形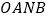 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线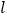 的方程.
的方程. -
科目: 来源: 题型:
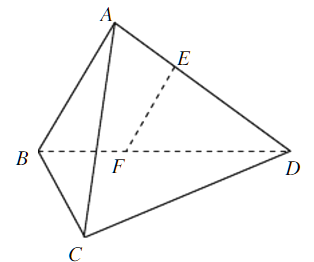
查看答案和解析>>【题目】如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10
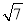 cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有质地、大小完全相同的5个小球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏.甲先摸出一个球.记下编号,放回后再摸出一个球,记下编号,如果两个编号之和为偶数.则算甲赢,否则算乙赢.
(1)求甲赢且编号之和为6的事件发生的概率:
(2)试问:这种游戏规则公平吗.请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°).
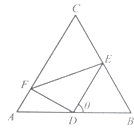
(1)当tan∠DEF=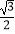 时,求θ的大小;
时,求θ的大小;
(2)求△DEF的面积S的最小值及使得S取最小值时θ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,若输入S的值为﹣1,则输出S的值为( )

A.﹣1
B.
C.2
D.3
相关试题

