【题目】袋中有质地、大小完全相同的5个小球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏.甲先摸出一个球.记下编号,放回后再摸出一个球,记下编号,如果两个编号之和为偶数.则算甲赢,否则算乙赢.
(1)求甲赢且编号之和为6的事件发生的概率:
(2)试问:这种游戏规则公平吗.请说明理由.
参考答案:
【答案】
(1)解:由题意知本题是一个古典概型,
试验发生包含的甲、乙两人取出的数字共有5×5=25(个)等可能的结果,
设“两个编号和为6”为事件A,
则事件A包含的基本事件为(1,5),(2,4),(3,3),(4,2),(5,1)共5个,
根据古典概型概率公式得到P(A)= ![]() =
= ![]()
(2)解:这种游戏规则是不公平的.
设甲胜为事件B,乙胜为事件C,
则甲胜即两编号和为偶数所包含的基本事件数有13个:
(1,1),(1,3),(1,5),(2,2),(2,4),
(3,1),(3,3),(3,5),(4,2),(4,4),
(5,1),(5,3),(5,5)
∴甲胜的概率P(B)= ![]()
乙胜的概率P(C)=1﹣P(B)= ![]()
∴这种游戏规则是不公平的
【解析】(1)本题是一个古典概型,试验发生包含的甲、乙两人取出的数字共有5×5种等可能的结果,满足条件的事件可以通过列举法得到,根据古典概型的概率公式得到结果.(2)要判断这种游戏是否公平,只要做出甲胜和乙胜的概率,先根据古典概型做出甲胜的概率,再由1减去甲胜的概率,得到乙胜的概率,得到两个人胜的概率相等,得到结论.
-
科目: 来源: 题型:
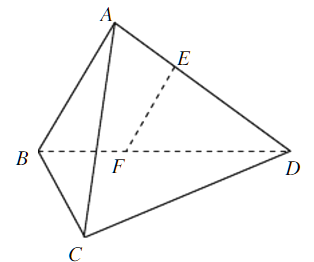
查看答案和解析>>【题目】如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10
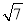 cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.

(Ⅰ)求BD的长;
(Ⅱ)求sin∠CBD的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°).
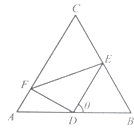
(1)当tan∠DEF=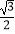 时,求θ的大小;
时,求θ的大小;
(2)求△DEF的面积S的最小值及使得S取最小值时θ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,若输入S的值为﹣1,则输出S的值为( )

A.﹣1
B.
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2
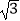 sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0,
sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0,  ]上的最大值和最小值;
]上的最大值和最小值;
(Ⅱ)若f(x0)=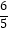 ,x0∈[
,x0∈[  ,
,  ],求cos2x0的值.
],求cos2x0的值.
相关试题

