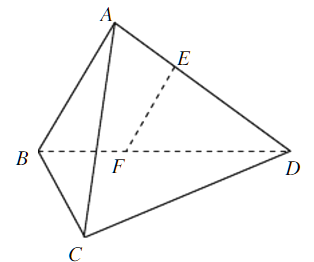
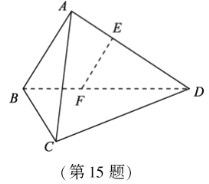
【题目】如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
参考答案:
【答案】(1)在平面![]() 内,AB⊥AD,
内,AB⊥AD,![]() ,则
,则![]() .∵
.∵![]() 平面ABC,
平面ABC,![]() 平面ABC,∴EF∥平面ABC.
平面ABC,∴EF∥平面ABC.
(2)∵BC⊥BD,平面![]() 平面BCD=BD,平面ABD⊥平面BCD,
平面BCD=BD,平面ABD⊥平面BCD,![]() 平面BCD,∴
平面BCD,∴![]() 平面
平面![]() .∵
.∵![]() 平面
平面![]() ,∴
,∴![]()
![]() .∵AB⊥AD,
.∵AB⊥AD,![]() 平面ABC,
平面ABC,![]() ,∴AD⊥平面ABC,又AC
,∴AD⊥平面ABC,又AC![]() 平面ABC,∴AD⊥AC.
平面ABC,∴AD⊥AC.
【解析】
证明:(1)在平面![]() 内,因为AB⊥AD,
内,因为AB⊥AD,![]() ,所以
,所以![]() .
.
 又因为
又因为![]() 平面ABC,
平面ABC,![]() 平面ABC,所以EF∥平面ABC.
平面ABC,所以EF∥平面ABC.
(2)因为平面ABD⊥平面BCD,
平面![]() 平面BCD=BD,
平面BCD=BD,
![]() 平面BCD,
平面BCD,![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
![]() .
.
又AB⊥AD,![]() ,
,![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
所以AD⊥平面ABC,
又因为AC![]() 平面ABC,
平面ABC,
所以AD⊥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
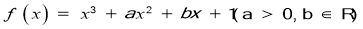 有极值,且导函数
有极值,且导函数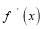 的极值点是
的极值点是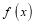 的零点。(极值点是指函数取极值时对应的自变量的值)
的零点。(极值点是指函数取极值时对应的自变量的值)求b关于a的函数关系式,并写出定义域;
证明:b>3a;
若
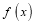 ,
,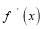 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于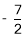 ,求a的取值范围。
,求a的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,椭圆
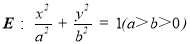 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为 ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
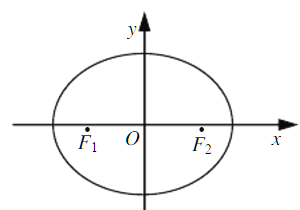
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
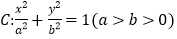 的短轴长为
的短轴长为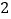 ,椭圆
,椭圆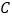 上任意一点到右焦点
上任意一点到右焦点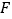 距 离的最大值为
距 离的最大值为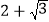 .
.(Ⅰ)求椭圆
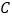 的标准方程;
的标准方程;(Ⅱ)过点
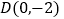 作直线
作直线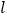 与曲线
与曲线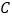 交于
交于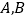 两点,点
两点,点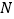 满足
满足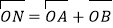 (
(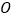 为坐标原点),求四边形
为坐标原点),求四边形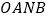 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线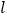 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10
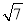 cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.

(Ⅰ)求BD的长;
(Ⅱ)求sin∠CBD的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有质地、大小完全相同的5个小球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏.甲先摸出一个球.记下编号,放回后再摸出一个球,记下编号,如果两个编号之和为偶数.则算甲赢,否则算乙赢.
(1)求甲赢且编号之和为6的事件发生的概率:
(2)试问:这种游戏规则公平吗.请说明理由.
相关试题

