【题目】设圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,且直线x-y+1=0被圆截得的弦长为2![]() ,求圆的方程.
,求圆的方程.
参考答案:
【答案】(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244.
【解析】试题分析:用待定系数法求解。设圆的方程为(x-a)2+(y-b)2=r2,根据圆心在直线![]() 上,点A(2,3)在圆上及弦长得到关于a,b,r的方程组,解方程组求得参数即可得到圆的方程。
上,点A(2,3)在圆上及弦长得到关于a,b,r的方程组,解方程组求得参数即可得到圆的方程。
试题解析:
设圆的方程为(x-a)2+(y-b)2=r2,
由题意,知直线x+2y=0过圆心,
∴a+2b=0.①
又点A在圆上,
∴(2-a)2+(3-b)2=r2.②
∵直线x-y+1=0被圆截得的弦长为![]() ,
,
∴ (![]() )2+
)2+![]() 2=r2.③
2=r2.③
由①②③可得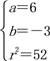 或
或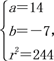
故所求圆的方程为(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244.
-
科目: 来源: 题型:
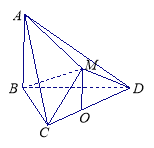
查看答案和解析>>【题目】如图,在多面体
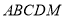 中,△
中,△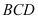 是等边三角形,△
是等边三角形,△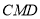 是等腰直角三角形,
是等腰直角三角形, ,平面
,平面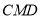
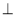 平面
平面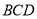 ,
,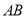
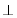 平面
平面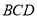 ,点
,点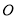 为
为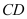 的中点,连接
的中点,连接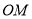 .
.
(1)求证:
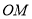 ∥平面
∥平面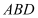 ;
;(2)若
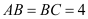 ,求三棱锥
,求三棱锥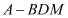 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
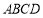 中,点
中,点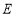 ,
,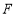 分别是
分别是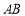 ,
,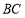 的中点,将
的中点,将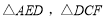 分别沿
分别沿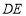 ,
,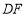 折起,使
折起,使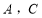 两点重合于
两点重合于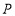 .
.
(Ⅰ)求证:平面
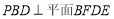 ;
;(Ⅱ)求二面角
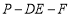 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 的方程为
的方程为 ,其中
,其中 .
. (1)求证:直线
 恒过定点;
恒过定点;(2)当
 变化时,求点
变化时,求点 到直线
到直线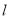 的距离的最大值;
的距离的最大值;(3)若直线
 分别与
分别与 轴、
轴、 轴的负半轴交于
轴的负半轴交于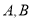 两点,求
两点,求 面积的最小值及此时直线
面积的最小值及此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
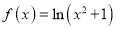 ,
, 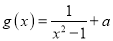
(1)若
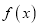 的一个极值点到直线
的一个极值点到直线 的距离为1,求
的距离为1,求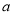 的值;
的值;(2)求方程
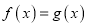 的根的个数
的根的个数 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
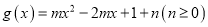 在
在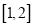 上有最大值1和最小值0,设
上有最大值1和最小值0,设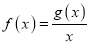 .
.(1)求
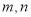 的值;
的值;(2)若不等式
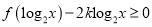 在
在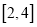 上有解,求实数
上有解,求实数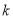 的取值范围;
的取值范围;(3)若方程
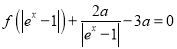 (
(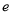 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数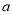 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
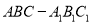 中,底面
中,底面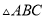 是边长为2的等边三角形,
是边长为2的等边三角形, 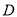 为
为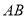 的中点.
的中点.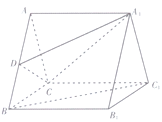
(1)求证:
 平面
平面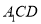 ;
;(2)若四边形
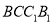 是正方形,且
是正方形,且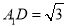 ,求直线
,求直线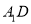 与平面
与平面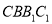 所成角的正弦值.
所成角的正弦值.
相关试题

