【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)![]() 时,利用导数与单调性的关系,对函数求导,并与零作比较可得函数的单调区间;(2)对函数求导,对参数
时,利用导数与单调性的关系,对函数求导,并与零作比较可得函数的单调区间;(2)对函数求导,对参数![]() 分类讨论,利用函数的单调性求函数的最小值,使最小值小于或等于零,可得
分类讨论,利用函数的单调性求函数的最小值,使最小值小于或等于零,可得![]() 的取值范围.
的取值范围.
试题解析:(1)当![]() 时,
时,![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() .
.
(2)要使![]() 在
在![]() 上有解,只要
上有解,只要![]() 在区间
在区间![]() 上的最小值小于等于0.
上的最小值小于等于0.
因为![]() ,
,
令![]() ,得
,得![]() ,
,![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
∴![]() .
.
②当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上最小值为
上最小值为![]() .
.
由![]() ,解得
,解得![]() ,
,
∴![]() .
.
综上可知,实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 “一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高),现从参赛者中抽取了
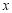 人,按年龄分成5组(第一组:
人,按年龄分成5组(第一组: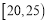 ,第二组
,第二组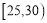 ,第三组:
,第三组: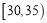 ,第四组:
,第四组: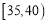 ,第五组:
,第五组: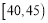 ),得到如图所示的频率分布直方图,已知第一组有6人.
),得到如图所示的频率分布直方图,已知第一组有6人.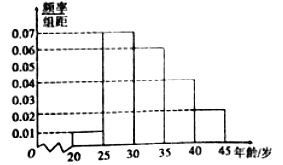
(1)求
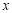 ;
;(2)求抽取的
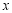 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);(3)从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1-5组,从这5个按年龄分的组合5个按职业分的组中每组各选派1人参加知识竞赛代表相应组的成绩,年龄组中1-5组的成绩分别为93,96,97,94,90,职业组中1-5组的成绩分别为93,98,94,95,90.
(i)分别求5个年龄组和5个职业组成绩的平均数和方差;
(ii)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度,并谈谈你的感想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
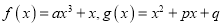 .
.(Ⅰ)若函数
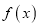 在
在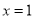 处取得极值,求实数
处取得极值,求实数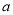 的值;
的值;(Ⅱ)在(Ⅰ)的条件下,函数
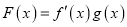 (其中
(其中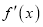 为函数
为函数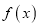 的导数)的图像关于直线
的导数)的图像关于直线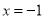 对称,求函数
对称,求函数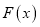 单调区间;
单调区间;(Ⅲ)在(Ⅱ)的条件下,若对任意的
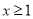 ,都有
,都有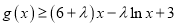 恒成立,求实数
恒成立,求实数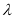 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设P是圆
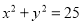 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且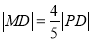 ,
,(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为
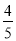 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.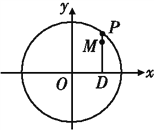
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面为直角梯形,
的底面为直角梯形,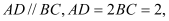
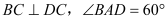 ,平面
,平面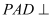 底面
底面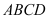 ,
,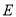 为
为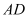 的中点,
的中点,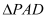 为正三角形,
为正三角形,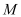 是棱
是棱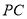 上的一点(异于端点).
上的一点(异于端点).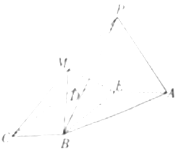
(Ⅰ)若
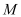 为
为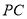 中点,求证:
中点,求证: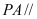 平面
平面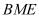 ;
;(Ⅱ)是否存在点
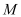 ,使二面角
,使二面角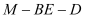 的大小为30°.若存在,求出点
的大小为30°.若存在,求出点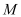 的位置;若不存在,说明理由.
的位置;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下茎叶图记录了甲,乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以
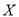 表示.
表示.
(1)如果
 ,求乙组同学植树棵数的平均数和方差;
,求乙组同学植树棵数的平均数和方差;(2)如果
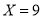 ,分别从甲,乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.(注:方差
,分别从甲,乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.(注:方差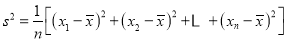 ,其中
,其中 为
为 ,
, 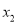 ,……,
,……,  的平均数)
的平均数) -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(Ⅰ)若教学满意度不低于9.5分,则称该生对教师的教学满意度为“极满意”.求从这16人中随机选取3人,至少有1人是“极满意”的概率;
(Ⅱ)以这16人的样本数据来估计整个学校的总体数据,若从该校所有学生中(学生人数很多)任选3人,记
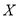 表示抽到“极满意”的人数,求
表示抽到“极满意”的人数,求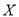 的分布列及数学期望.
的分布列及数学期望.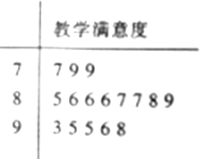
相关试题

