【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,函数![]() (其中
(其中![]() 为函数
为函数![]() 的导数)的图像关于直线
的导数)的图像关于直线![]() 对称,求函数
对称,求函数![]() 单调区间;
单调区间;
(Ⅲ)在(Ⅱ)的条件下,若对任意的![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)函数
;(Ⅱ)函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;(Ⅲ)
上单调递减;(Ⅲ) ![]() .
.
【解析】
试题分析:(Ⅰ)由![]() ,得
,得![]() ;(Ⅱ)
;(Ⅱ)![]() 的图象关于直线
的图象关于直线![]() 对称,故函数
对称,故函数![]() 为偶函数,解得
为偶函数,解得![]() ,分别令
,分别令![]() ,
,![]() 即可得到单调区间;(Ⅲ)对任意的
即可得到单调区间;(Ⅲ)对任意的![]() ,都有
,都有![]() 恒成立可转化为
恒成立可转化为![]() 在
在![]() 上恒成立,易知
上恒成立,易知![]() ,∴
,∴![]() 在
在![]() 上恒成立,构造函数
上恒成立,构造函数![]() ,只需
,只需![]() 即可.
即可.
试题解析:(Ⅰ)由![]() 有
有![]()
因为![]() 在
在![]() 处取得极值,故
处取得极值,故![]()
∴![]()
经检验:当![]() 时,符合题意,故
时,符合题意,故![]() .
.
(Ⅱ)由(Ⅰ)知:![]()
∵![]() 的图像关于直线
的图像关于直线![]() 对称,故函数
对称,故函数![]() 为偶函数
为偶函数
又![]()
![]()
∴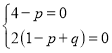 ,解得
,解得![]()
∴![]()
∴![]()
令![]() 有
有![]() 或
或![]()
令![]() 有
有![]() 或
或![]()
∴函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
在区间![]() 上单调递减.
上单调递减.
(Ⅲ)由(Ⅱ)知,对任意的![]() ,都有
,都有![]() 恒成立可转化为
恒成立可转化为
![]() 在
在![]() 上恒成立
上恒成立
易知![]() ∴
∴![]() 在
在![]() 上恒成立
上恒成立
令![]() ,∴
,∴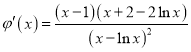
令![]() ,∴
,∴![]()
∴![]() 在
在![]() 上递减,
上递减,![]() 上递增
上递增
∴![]()
∴![]() ,即
,即![]() 在
在![]() 上递增
上递增
∴![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
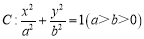 的左、右焦点分别为
的左、右焦点分别为 ,
, ,椭圆上一点
,椭圆上一点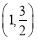 与椭圆右焦点的连线垂直于
与椭圆右焦点的连线垂直于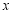 轴.
轴.(1)求椭圆
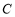 的方程;
的方程;(2)与抛物线
 相切于第一象限的直线
相切于第一象限的直线 ,与椭圆
,与椭圆 交于
交于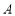 ,
, 两点,与
两点,与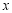 轴交于点
轴交于点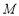 ,线段
,线段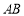 的垂直平分线与
的垂直平分线与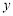 轴交于点
轴交于点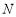 ,求直线
,求直线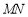 斜率的最小值.
斜率的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对绵阳南山实验学校的500名教师的年龄进行统计分析,年龄的频率分布直方图如图所示,规定年龄在
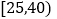 内的为青年教师,
内的为青年教师,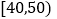 内的为中年教师,
内的为中年教师,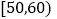 内的为老年教师.
内的为老年教师.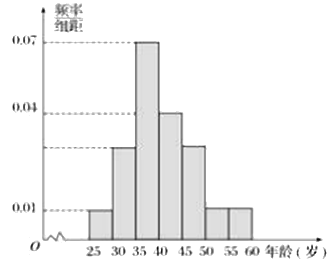
(1)求年龄
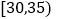 ,
,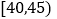 内的教师人数;
内的教师人数;(2)现用分层抽样的方法从中、青年中抽取18人进行同课异构课堂展示,求抽到年龄在
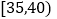 内的人数.
内的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】 “一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高),现从参赛者中抽取了
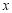 人,按年龄分成5组(第一组:
人,按年龄分成5组(第一组: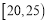 ,第二组
,第二组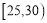 ,第三组:
,第三组: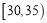 ,第四组:
,第四组: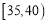 ,第五组:
,第五组: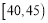 ),得到如图所示的频率分布直方图,已知第一组有6人.
),得到如图所示的频率分布直方图,已知第一组有6人.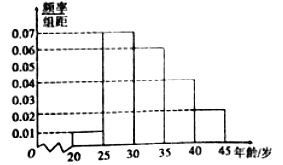
(1)求
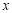 ;
;(2)求抽取的
 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);(3)从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1-5组,从这5个按年龄分的组合5个按职业分的组中每组各选派1人参加知识竞赛代表相应组的成绩,年龄组中1-5组的成绩分别为93,96,97,94,90,职业组中1-5组的成绩分别为93,98,94,95,90.
(i)分别求5个年龄组和5个职业组成绩的平均数和方差;
(ii)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度,并谈谈你的感想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设P是圆
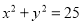 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且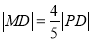 ,
,(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为
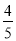 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.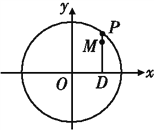
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
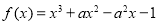 ,
,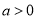 .
.(1)当
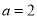 时,求函数
时,求函数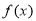 的单调区间;
的单调区间;(2)若关于
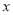 的不等式
的不等式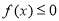 在
在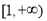 上有解,求实数
上有解,求实数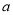 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
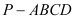 的底面为直角梯形,
的底面为直角梯形,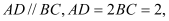
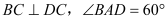 ,平面
,平面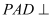 底面
底面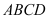 ,
,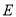 为
为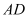 的中点,
的中点,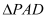 为正三角形,
为正三角形,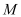 是棱
是棱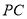 上的一点(异于端点).
上的一点(异于端点).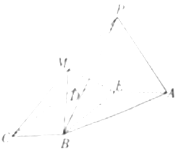
(Ⅰ)若
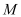 为
为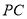 中点,求证:
中点,求证: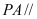 平面
平面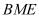 ;
;(Ⅱ)是否存在点
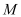 ,使二面角
,使二面角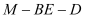 的大小为30°.若存在,求出点
的大小为30°.若存在,求出点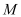 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
相关试题

