【题目】若异面直线![]() 所成的角是
所成的角是![]() ,则以下三个命题:
,则以下三个命题:
①存在直线![]() ,满足
,满足![]() 与
与![]() 的夹角都是
的夹角都是![]() ;
;
②存在平面![]() ,满足
,满足![]() ,
,![]() 与
与![]() 所成角为
所成角为![]() ;
;
③存在平面![]() ,满足
,满足![]() ,
,![]() 与
与![]() 所成锐二面角为
所成锐二面角为![]() .
.
其中正确命题的个数为( )
A. 0 B. 1 C. 2 D. 3
参考答案:
【答案】D
【解析】分析:在①中,在![]() 上任取一点
上任取一点![]() ,过
,过![]() 作
作![]() ,
, ![]() 与
与![]() 的夹角均为
的夹角均为![]() ;在②中,在
;在②中,在![]() 上取一点
上取一点![]() ,过
,过![]() 作
作![]() ;在③中,在
;在③中,在![]() 上取一点
上取一点![]() ,过
,过![]() 作
作![]() ,
,![]() 确定一个平面平面
确定一个平面平面![]() 即可.
即可.
详解:异面直线![]() 所成的角是
所成的角是![]() ,在①中,由异面直线
,在①中,由异面直线![]() 所成的角是
所成的角是![]() ,
,
在![]() 上任取一点
上任取一点![]() ,过
,过![]() 作
作![]() ,在空间中过点
,在空间中过点![]() 能作出直线
能作出直线![]() ,使得
,使得![]() 与
与![]() 的夹角均为
的夹角均为![]() ,
,![]() 存在直线
存在直线![]() ,满足
,满足![]() 与
与![]() 的夹角都是
的夹角都是![]() ,故①正确;
,故①正确;
在②中,在![]() 上取一点
上取一点![]() ,过
,过![]() 作
作![]() ,则以
,则以![]() 确定的平面
确定的平面![]() ,满足
,满足![]() 与
与![]()
所成的角是![]() ,故②正确;在③中,在
,故②正确;在③中,在![]() 上取一点
上取一点![]() ,过
,过![]() 作
作![]() ,
,![]() 确定一个平面平面
确定一个平面平面![]() ,过
,过![]() 能作出一个平面
能作出一个平面![]() ,满足
,满足![]() 与
与![]() 所成锐二面角为
所成锐二面角为![]() ,故③正确,故选D
,故③正确,故选D
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
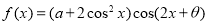 为奇函数,且
为奇函数,且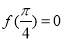 ,其中
,其中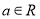 ,
,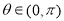 .
.(1)求
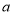 ,
,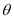 的值.
的值.(2)若
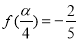 ,
,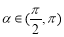 ,求
,求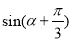 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知点
 在椭圆
在椭圆 上,将射线
上,将射线 绕原点
绕原点 逆时针旋转
逆时针旋转 ,所得射线
,所得射线 交直线
交直线 于点
于点 .以
.以 为极点,
为极点, 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.(1)求椭圆
 和直线
和直线 的极坐标方程;
的极坐标方程;(2)证明::
 中,斜边
中,斜边 上的高
上的高 为定值,并求该定值.
为定值,并求该定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
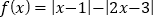 .
.(1)求不等式
 的解集;
的解集;(2)设
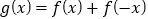 ,求
,求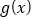 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在各棱长均为2的三棱柱
 中,侧面
中,侧面 底面ABC,
底面ABC, .
.(1)求侧棱
 与平面
与平面 所成角的正弦值的大小;
所成角的正弦值的大小;(2)已知点D满足
 ,在直线
,在直线 上是否存在点P,使DP∥平面
上是否存在点P,使DP∥平面 ?若存在,请确定点P的位置,若不存在,请说明理由.
?若存在,请确定点P的位置,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】盒子中仅有4个白球和5个黑球,从中任意取出一个球.
(1)“取出的球是黄球”是什么事件?它的概率是多少?
(2)“取出的球是白球”是什么事件?它的概率是多少?
(3)“取出的球是白球或黑球”是什么事件?它的概率是多少?
(4)设计一个用计算器或计算机模拟上面取球的试验,并模拟100次,估计“取出的球是白球”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】连续抛掷同一颗骰子3次,则3次掷得的点数之和为9的概率是____.
相关试题

