【题目】盒子中仅有4个白球和5个黑球,从中任意取出一个球.
(1)“取出的球是黄球”是什么事件?它的概率是多少?
(2)“取出的球是白球”是什么事件?它的概率是多少?
(3)“取出的球是白球或黑球”是什么事件?它的概率是多少?
(4)设计一个用计算器或计算机模拟上面取球的试验,并模拟100次,估计“取出的球是白球”的概率.
参考答案:
【答案】(1)答案见解析.(2)答案见解析.(3)答案见解析.(4)答案见解析.
【解析】
(1)"袋中没有黄球,故摸出的球是黄球"是不可能事件;
(2)"摸出的球是白球"是不确定事件,根据概率公式即可求解;
(3)"摸出的球是白球或黑球"是必然事件,故它的概率为![]() ;
;
(4)利用计算机生成随机数表,即可估计估计“取出的球是白球”的概率.
(1)从中任意取出一个球,“取出的球是黄球”是不可能事件,它的概率为![]() .
.
(2)“取出的球是白球”是随机事件事件,它的概率是![]() .
.
(3)“取出的球是白球或是黑球”是必然事件,它的概率是![]()
(4)用计算机产生1-9的随机数,规定1-4代表白球,5-9代表黑球.
7 | 6 | 8 | 4 | 1 |
3 | 8 | 1 | 6 | 4 |
8 | 6 | 8 | 4 | 8 |
8 | 4 | 6 | 2 | 1 |
5 | 1 | 5 | 5 | 2 |
2 | 8 | 3 | 6 | 5 |
9 | 4 | 3 | 5 | 7 |
9 | 7 | 9 | 5 | 3 |
3 | 4 | 4 | 3 | 4 |
4 | 8 | 4 | 9 | 2 |
4 | 9 | 2 | 1 | 1 |
6 | 4 | 5 | 5 | 2 |
7 | 8 | 4 | 3 | 4 |
9 | 6 | 9 | 8 | 4 |
6 | 7 | 5 | 8 | 9 |
9 | 4 | 8 | 6 | 8 |
7 | 3 | 7 | 1 | 3 |
8 | 3 | 2 | 6 | 6 |
4 | 3 | 1 | 7 | 7 |
2 | 2 | 4 | 9 | 5 |
从表中可以查1-4数据有46个, 5-9数据有54个.
![]() “取出的球是白球”的概率为:
“取出的球是白球”的概率为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
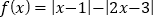 .
.(1)求不等式
 的解集;
的解集;(2)设
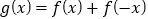 ,求
,求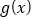 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若异面直线
 所成的角是
所成的角是 ,则以下三个命题:
,则以下三个命题:①存在直线
 ,满足
,满足 与
与 的夹角都是
的夹角都是 ;
;②存在平面
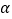 ,满足
,满足 ,
, 与
与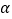 所成角为
所成角为 ;
;③存在平面
 ,满足
,满足 ,
,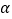 与
与 所成锐二面角为
所成锐二面角为 .
.其中正确命题的个数为( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在各棱长均为2的三棱柱
 中,侧面
中,侧面 底面ABC,
底面ABC, .
.(1)求侧棱
 与平面
与平面 所成角的正弦值的大小;
所成角的正弦值的大小;(2)已知点D满足
 ,在直线
,在直线 上是否存在点P,使DP∥平面
上是否存在点P,使DP∥平面 ?若存在,请确定点P的位置,若不存在,请说明理由.
?若存在,请确定点P的位置,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】连续抛掷同一颗骰子3次,则3次掷得的点数之和为9的概率是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
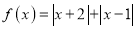 .
.(Ⅰ)求
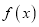 的最小值及取得最小值时
的最小值及取得最小值时 的取值范围;
的取值范围;(Ⅱ)若集合
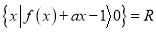 ,求实数
,求实数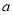 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】
已知公比为整数的正项等比数列
 满足:
满足:  ,
,  .
.(1)求数列
 的通项公式;
的通项公式;(2)令
 ,求数列
,求数列 的前
的前 项和
项和 .
.
相关试题

