【题目】已知 函数f(x)=x3+(m﹣4)x2﹣3mx+(n﹣6)x∈R的图象关于原点对称,其中m,n为实常数.
(1)求m,n的值;
(2)试用单调性的定义证明:f(x)在区间[﹣2,2]上是单调函数;
(3)当﹣2≤x≤2 时,不等式f(x)≥(n﹣logma)logma恒成立,求实数a的取值范围.
参考答案:
【答案】
(1)解:由已知得f(x)为奇函数∴f(﹣x)=﹣f(x)即﹣x3+(m﹣4)x2+3mx+(n﹣6)=﹣x3﹣(m﹣4)x2+3mx﹣(n﹣6)恒成立,即(m﹣4)x2+(n﹣6)=0恒成立,∴m=4,n=6
(2)解:由(1)的f(x)=x3﹣12x,设﹣2≤x1<x2≤2, ![]() ,
,
∵﹣2≤x1<x2≤2,∴ ![]() ,
,
∴f(x1)﹣f(x2)>0,
即∴f(x1)>f(x2),
∴f(x)在[﹣2,2]上是减函数
(3)解:由(2)知f(x)在[﹣2,2]上是减函数,
则f(x)≥f(2)=﹣16﹣16≥(6﹣log4a)log4a,
∴(log4a﹣8)(log4a+2)≥0,
∴log4a≤﹣2或log4a≥8,
∴ ![]() 或a≥48
或a≥48
【解析】(1)利用函数的对称性,得到方程,转化求解m,n即可.(2)利用函数的单调性的定义直接证明即可.(3)利用函数的单调性结合函数的定义域,转化求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程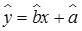 .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求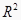 并说明模型的拟合效果.
并说明模型的拟合效果. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+a(x﹣1)2,其中a>0.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)讨论函数f(x)的单调性;
(3)若函数f(x)有两个极值点x1,x2,且x1<x2,求证:
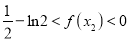 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧面
中,侧面 底面
底面 ,且
,且 ,
,  ,
,  ,
,  是
是 的中点.
的中点.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cos∠B=
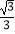
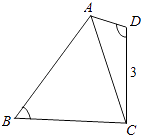
(1)求△ACD的面积;
(2)若BC=2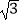 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形
 中,
中,  点
点 是
是 边的中点,将
边的中点,将 沿
沿 折起,使平面
折起,使平面 平面
平面 ,连接
,连接 得到如图
得到如图 所示的几何体.
所示的几何体.
(1)求证;
 平面
平面 ;
;(2)若
 二面角
二面角 的平面角的正切值为
的平面角的正切值为 求二面角
求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
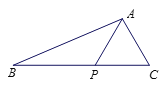
查看答案和解析>>【题目】如图, 在△
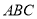 中, 点
中, 点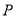 在
在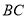 边上,
边上, 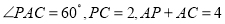 .
.(Ⅰ)求
 ;
;(Ⅱ)若△
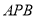 的面积是
的面积是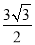 , 求
, 求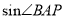 .
.
相关试题

