【题目】已知函数f(x)=lnx+a(x﹣1)2,其中a>0.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)讨论函数f(x)的单调性;
(3)若函数f(x)有两个极值点x1,x2,且x1<x2,求证: ![]() .
.
参考答案:
【答案】(1)切线方程:y=x﹣1,(2)见解析,(3)见解析.
【解析】试题分析:(1)当a=1时,求出f(1),然后得到取得坐标,求出函数的导数,求出切线的斜率,然后求解切线方程;(2)求出函数的导数,通过a的讨论,判断导函数的符号,然后求解函数f(x)的单调性;(3)利用函数的极值点以及函数的单调性,转化证明即可.
(1)当a=1时,f(1)=0,f′(x)=![]() +2(x﹣1),f′(1)=1,
+2(x﹣1),f′(1)=1,
曲线y=f(x)在点(1,0)处的切线方程:y=x﹣1.
(2)∵f(x)=lnx+ax2﹣2ax+a ![]() (x>0)
(x>0)
①当△=4a2﹣8a≤0即0<a≤2时,f′(x)>0,
∴f(x)的单调递增区间是(0.+∞).
②当△=4a2﹣8a>0时,即a>2时,令f′(x)=0得![]() .
.
∴f(x)的单调递增区间是(x2,+∞)和(0,x1),单调递减区间是(x1,x2).
(3)证明:∵f(x)在(x2,+∞)单调递增,且x2<1,
∴f(x2)<f(1)=0,不等式右侧证毕。′
∵f(x)有两个极值点x1,x2,∴a>2.故![]() ,
,
令![]() ,
, ![]()
∴g(x)在(![]() )单调递增.
)单调递增. ![]() 故
故![]()
不等式左侧证毕.综上可知: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作
不太主动参加班级工作
合计
学习积极性高
18
7
25
学习积极性一般
6
19
25
合计
24
26
50
参考公式及数据:
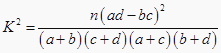
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln(2+x),g(x)=ln(2﹣x)
(1)判断函数h(x)=f(x)﹣g(x)的奇偶性;
(2)求使f(x)≥g(x)成立的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程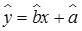 .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求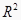 并说明模型的拟合效果.
并说明模型的拟合效果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧面
中,侧面 底面
底面 ,且
,且 ,
,  ,
,  ,
,  是
是 的中点.
的中点.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知 函数f(x)=x3+(m﹣4)x2﹣3mx+(n﹣6)x∈R的图象关于原点对称,其中m,n为实常数.
(1)求m,n的值;
(2)试用单调性的定义证明:f(x)在区间[﹣2,2]上是单调函数;
(3)当﹣2≤x≤2 时,不等式f(x)≥(n﹣logma)logma恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cos∠B=
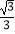
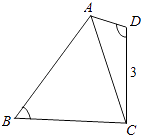
(1)求△ACD的面积;
(2)若BC=2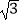 ,求AB的长.
,求AB的长.
相关试题

