【题目】如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cos∠B= ![]()
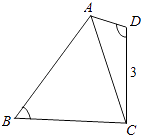
(1)求△ACD的面积;
(2)若BC=2 ![]() ,求AB的长.
,求AB的长.
参考答案:
【答案】
(1)解:因为∠D=2∠B,cos∠B= ![]() ,
,
所以cosD=cos2B=2cos2B﹣1=﹣ ![]() .
.
因为∠D∈(0,π),
所以sinD= ![]() .
.
因为 AD=1,CD=3,
所以△ACD的面积S= ![]() =
= ![]() =
= ![]() .
.
(2)解:在△ACD中,AC2=AD2+DC2﹣2ADDCcosD=12.
所以AC=2 ![]() .
.
因为BC=2 ![]() ,
, ![]() ,
,
所以 ![]() =
= ![]() .
.
所以 AB=4.
【解析】(1)利用已知条件求出D角的正弦函数值,然后求△ACD的面积;(2)利用余弦定理求出AC,通过BC=2 ![]() ,利用正弦定理求解AB的长.
,利用正弦定理求解AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+a(x﹣1)2,其中a>0.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)讨论函数f(x)的单调性;
(3)若函数f(x)有两个极值点x1,x2,且x1<x2,求证:
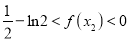 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧面
中,侧面 底面
底面 ,且
,且 ,
,  ,
,  ,
,  是
是 的中点.
的中点.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知 函数f(x)=x3+(m﹣4)x2﹣3mx+(n﹣6)x∈R的图象关于原点对称,其中m,n为实常数.
(1)求m,n的值;
(2)试用单调性的定义证明:f(x)在区间[﹣2,2]上是单调函数;
(3)当﹣2≤x≤2 时,不等式f(x)≥(n﹣logma)logma恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形
 中,
中,  点
点 是
是 边的中点,将
边的中点,将 沿
沿 折起,使平面
折起,使平面 平面
平面 ,连接
,连接 得到如图
得到如图 所示的几何体.
所示的几何体.
(1)求证;
 平面
平面 ;
;(2)若
 二面角
二面角 的平面角的正切值为
的平面角的正切值为 求二面角
求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
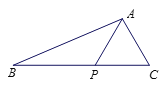
查看答案和解析>>【题目】如图, 在△
 中, 点
中, 点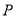 在
在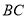 边上,
边上, 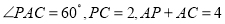 .
.(Ⅰ)求
 ;
;(Ⅱ)若△
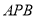 的面积是
的面积是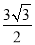 , 求
, 求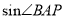 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12
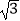 海里;在A处看灯塔C在货轮的北偏西30°,距离为8
海里;在A处看灯塔C在货轮的北偏西30°,距离为8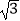 海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
相关试题

