【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程 ![]() .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求 ![]() 并说明模型的拟合效果.
并说明模型的拟合效果.
参考答案:
【答案】
(1)
解:将已知条件制成下表:
i | 1 | 2 | 3 | 4 | 5 | 合计 |
| 2 | 3 | 4 | 5 | 6 | 20 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 | 25 |
| 4.4 | 11.4 | 22.0 | 32.5 | 42.0 | 112.3 |
| 4 | 9 | 16 | 25 | 36 | 90 |
![]()
于是有 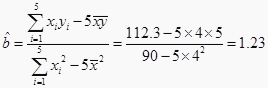 ,
,
![]() ,
,
回归直线方程是 ![]() .
.
(2)
解:当x=10时,y=1.23×10+0.08=12.38(万元),即估计使用10年时维修费用是12.38万元.
(3)
解:总偏差平方和: ![]() ,残差平方和
,残差平方和 ![]() ,
,
回归平方和:15.78-0.651=15.129.
(4)
解: 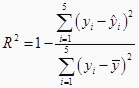
![]()
模型的拟合效果较好,使用年限解释了95.87%的维修费用支出
【解析】本题主要考查了回归分析的初步应用;实际推断原理和假设检验的应用,解决问题的关键是根据回归分析的初步应用的原理及实际推断分析计算即可解决问题.
-
科目: 来源: 题型:
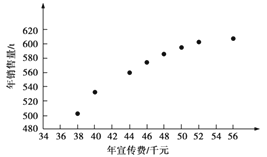
查看答案和解析>>【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及下面一些统计量的值.
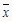
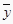
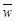
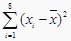
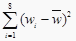
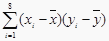
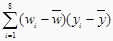
46.6
563
6.8
289.8
1.6
1469
108.8
表中
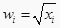 ,
, 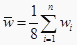 .
.
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最下二乘估计分别为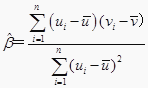 ,
, 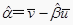 .
.
(1)根据散点图判断,y=a+bx与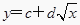 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果回答下列问题:
①年宣传费x=49时,年销售量及年利润的预报值时多少?
②年宣传费x为何值时,年利润的预报值最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作
不太主动参加班级工作
合计
学习积极性高
18
7
25
学习积极性一般
6
19
25
合计
24
26
50
参考公式及数据:
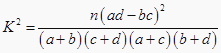
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln(2+x),g(x)=ln(2﹣x)
(1)判断函数h(x)=f(x)﹣g(x)的奇偶性;
(2)求使f(x)≥g(x)成立的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+a(x﹣1)2,其中a>0.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)讨论函数f(x)的单调性;
(3)若函数f(x)有两个极值点x1,x2,且x1<x2,求证:
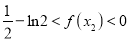 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧面
中,侧面 底面
底面 ,且
,且 ,
,  ,
,  ,
,  是
是 的中点.
的中点.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知 函数f(x)=x3+(m﹣4)x2﹣3mx+(n﹣6)x∈R的图象关于原点对称,其中m,n为实常数.
(1)求m,n的值;
(2)试用单调性的定义证明:f(x)在区间[﹣2,2]上是单调函数;
(3)当﹣2≤x≤2 时,不等式f(x)≥(n﹣logma)logma恒成立,求实数a的取值范围.
相关试题

