【题目】已知函数/(x![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 最小值;
最小值;
(2)若![]() 存在单调递减区间,求
存在单调递减区间,求![]() 的取值范围;
的取值范围;
(3)求证:![]() .
.
参考答案:
【答案】(1)1;(2)![]() ;(3)见解析
;(3)见解析
【解析】分析:(I)可先求f′(x),从而判断f(x)在x∈[1,+∞)上的单调性,利用其单调性求f(x)在x∈[1,+∞)最小值;(Ⅱ)求h′(x),可得![]() 若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:ax2+2(a﹣1)x+a<0有x>0的解.通过对a分a=0,a<0与当a>0三种情况讨论解得a的取值范围;(Ⅲ)(法一)根据(Ⅰ)的结论,当x>1时,
若f(x)存在单调递减区间,需h′(x)<0有正数解.从而转化为:ax2+2(a﹣1)x+a<0有x>0的解.通过对a分a=0,a<0与当a>0三种情况讨论解得a的取值范围;(Ⅲ)(法一)根据(Ⅰ)的结论,当x>1时,![]() ,即
,即![]() .,再构造函数,令
.,再构造函数,令![]() ,有
,有![]() ,从而
,从而![]() ,问题可解决;(法二)可用数学归纳法予以证明.当n=1时,ln(n+1)=ln2,3ln2=ln8>1
,问题可解决;(法二)可用数学归纳法予以证明.当n=1时,ln(n+1)=ln2,3ln2=ln8>1![]() ,成立;设
,成立;设![]() 时,命题成立,即
时,命题成立,即![]() ,,再去证明n=k+1时,
,,再去证明n=k+1时,![]() 即可(需用好归纳假设).
即可(需用好归纳假设).
详解:
(1)![]() ,定义域为
,定义域为![]() .
.
∵![]()
∴![]() 在
在![]() 上是增函数.
上是增函数.
![]() .
.
(2)因为![]()
因为若![]() 存在单调递减区间,所以
存在单调递减区间,所以![]() 有正数解.
有正数解.
即![]() 有
有![]() 有解.
有解.
①当![]() 时,明显成立.
时,明显成立.
②当![]() 时,
时,![]() 开口向下的抛物线,
开口向下的抛物线,![]() 总有
总有![]() 有解;
有解;
③当![]() 时,
时,![]() 开口向上的抛物线,即方程
开口向上的抛物线,即方程![]() 有正跟.
有正跟.
当![]() 时,
时,![]() ;
;
![]() ,解得
,解得![]() .
.
综合①②③知:![]() .
.
综上所述:![]() 的取值范围为
的取值范围为![]() .
.
(3)(法一)根据(1)的结论,当![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,则有
,则有![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(法二)当![]() 时,
时,![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() 时命题成立.
时命题成立.
设当![]() 时,命题成立,即
时,命题成立,即![]() .
.
∴![]() 时,
时,![]()
根据(1)的结论,当![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,则有
,则有![]() ,
,
则有![]() ,
,
即![]() 时命题也成立.
时命题也成立.
因此,由数学归纳法可知不等式成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,
 ,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号


A. 522B. 324C. 535D. 578
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表中的数据是一次阶段性考试某班的数学、物理原始成绩:

用这44人的两科成绩制作如下散点图:

学号为22号的
 同学由于严重感冒导致物理考试发挥失常,学号为31号的
同学由于严重感冒导致物理考试发挥失常,学号为31号的 同学因故未能参加物理学科的考试,为了使分析结果更客观准确,老师将
同学因故未能参加物理学科的考试,为了使分析结果更客观准确,老师将 两同学的成绩(对应于图中
两同学的成绩(对应于图中 两点)剔除后,用剩下的42个同学的数据作分析,计算得到下列统计指标:
两点)剔除后,用剩下的42个同学的数据作分析,计算得到下列统计指标:数学学科平均分为110.5,标准差为18.36,物理学科的平均分为74,标准差为11.18,数学成绩

与物理成绩
 的相关系数为
的相关系数为 ,回归直线
,回归直线 (如图所示)的方程为
(如图所示)的方程为 .
.(1)若不剔除
 两同学的数据,用全部44人的成绩作回归分析,设数学成绩
两同学的数据,用全部44人的成绩作回归分析,设数学成绩 与物理成绩
与物理成绩 的相关系数为
的相关系数为 ,回归直线为
,回归直线为 ,试分析
,试分析 与
与 的大小关系,并在图中画出回归直线
的大小关系,并在图中画出回归直线 的大致位置;
的大致位置;(2)如果
 同学参加了这次物理考试,估计
同学参加了这次物理考试,估计 同学的物理分数(精确到个位);
同学的物理分数(精确到个位);(3)就这次考试而言,学号为16号的
 同学数学与物理哪个学科成绩要好一些?(通常为了比较某个学生不同学科的成绩水平,可按公式
同学数学与物理哪个学科成绩要好一些?(通常为了比较某个学生不同学科的成绩水平,可按公式 统一化成标准分再进行比较,其中
统一化成标准分再进行比较,其中 为学科原始分,
为学科原始分, 为学科平均分,
为学科平均分, 为学科标准差).
为学科标准差). -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在
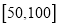 内,发布成绩使用等级制.各等级划分标准见下表.
内,发布成绩使用等级制.各等级划分标准见下表.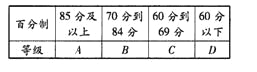
规定:
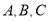 三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了
三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了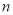 名学生的原始成绩作为样本进行统计.按照
名学生的原始成绩作为样本进行统计.按照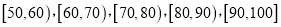 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.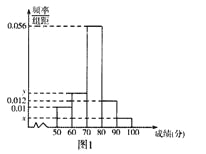
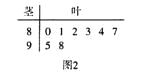
(I)求
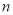 和频率分布直方图中的
和频率分布直方图中的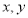 的值,并估计该校高一年级学生成绩是合格等级的概率;
的值,并估计该校高一年级学生成绩是合格等级的概率;(II)在选取的样本中,从
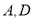 两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是
两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是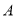 等级的概率.
等级的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 为奇函数.
为奇函数.(1)求b的值;
(2)证明:函数f(x)在区间(1,+∞)上是减函数;
(3)解关于x的不等式f(1+x2)+f(-x2+2x-4)>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (
( 为参数)与
为参数)与 轴正半轴,
轴正半轴, 轴正半轴的交点分别为
轴正半轴的交点分别为 ,动点
,动点 是椭圆上任一点,则
是椭圆上任一点,则 面积的最大值为( )
面积的最大值为( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】记[x]为不超过实数x的最大整数,例如,[2]=2,[1.5]=1,[﹣0.3]=﹣1.设a为正整数,数列{xn}满足x1=a,
 ,现有下列命题:
,现有下列命题:
①当a=5时,数列{xn}的前3项依次为5,3,2;
②对数列{xn}都存在正整数k,当n≥k时总有xn=xk;
③当n≥1时, ;
;
④对某个正整数k,若xk+1≥xk , 则 .
.
其中的真命题有 . (写出所有真命题的编号)
相关试题

