【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制.各等级划分标准见下表.
内,发布成绩使用等级制.各等级划分标准见下表.
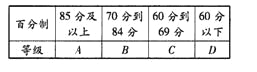
规定:![]() 三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了
三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计.按照
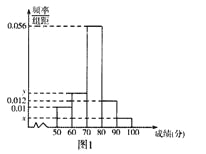
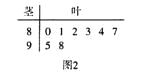
名学生的原始成绩作为样本进行统计.按照![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
(I)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值,并估计该校高一年级学生成绩是合格等级的概率;
的值,并估计该校高一年级学生成绩是合格等级的概率;
(II)在选取的样本中,从![]() 两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是
两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是![]() 等级的概率.
等级的概率.
参考答案:
【答案】(I)![]() ,
,![]() ;(II)
;(II)![]() .
.
【解析】
试题(I)根据频率直方图的相关概率易求![]() ,依据样本估计总体的思想可得该校高一年级学生成绩是合格等级的概率;(II)记“至少有一名学生是
,依据样本估计总体的思想可得该校高一年级学生成绩是合格等级的概率;(II)记“至少有一名学生是![]() 等级”事件为
等级”事件为![]() ,求事件
,求事件![]() 对立事件
对立事件![]() 的的概率,可得
的的概率,可得![]() .
.
试题解析:(I)由题意可知,样本容量![]()
![]()
因为成绩是合格等级人数为:![]() 人,抽取的50人中成绩是合格等级的频率为
人,抽取的50人中成绩是合格等级的频率为![]() ,依据样本估计总体的思想,所以,该校高一年级学生成绩是合格等级的概率为
,依据样本估计总体的思想,所以,该校高一年级学生成绩是合格等级的概率为![]()
(II)由茎叶图知,![]() 等级的学生共有3人,
等级的学生共有3人,![]() 等级学生共有
等级学生共有![]() 人,记
人,记![]() 等级的学生为
等级的学生为![]() ,
,
![]() 等级学生为
等级学生为![]() ,则从8名学生中随机抽取2名学生的所有情况为:
,则从8名学生中随机抽取2名学生的所有情况为:![]()
![]()
![]() 共28个基本事件
共28个基本事件
记“至少有一名学生是![]() 等级”事件为
等级”事件为![]() ,则事件
,则事件![]() 的可能结果为
的可能结果为![]()
![]()
![]() 共10种
共10种
因此![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 与等比数列
与等比数列 满足
满足 ,
, ,且
,且 .
. (1)求数列
 ,
, 的通项公式;
的通项公式;(2)设
 ,是否存在正整数
,是否存在正整数 ,使
,使 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,
 ,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号


A. 522B. 324C. 535D. 578
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表中的数据是一次阶段性考试某班的数学、物理原始成绩:

用这44人的两科成绩制作如下散点图:

学号为22号的
 同学由于严重感冒导致物理考试发挥失常,学号为31号的
同学由于严重感冒导致物理考试发挥失常,学号为31号的 同学因故未能参加物理学科的考试,为了使分析结果更客观准确,老师将
同学因故未能参加物理学科的考试,为了使分析结果更客观准确,老师将 两同学的成绩(对应于图中
两同学的成绩(对应于图中 两点)剔除后,用剩下的42个同学的数据作分析,计算得到下列统计指标:
两点)剔除后,用剩下的42个同学的数据作分析,计算得到下列统计指标:数学学科平均分为110.5,标准差为18.36,物理学科的平均分为74,标准差为11.18,数学成绩

与物理成绩
 的相关系数为
的相关系数为 ,回归直线
,回归直线 (如图所示)的方程为
(如图所示)的方程为 .
.(1)若不剔除
 两同学的数据,用全部44人的成绩作回归分析,设数学成绩
两同学的数据,用全部44人的成绩作回归分析,设数学成绩 与物理成绩
与物理成绩 的相关系数为
的相关系数为 ,回归直线为
,回归直线为 ,试分析
,试分析 与
与 的大小关系,并在图中画出回归直线
的大小关系,并在图中画出回归直线 的大致位置;
的大致位置;(2)如果
 同学参加了这次物理考试,估计
同学参加了这次物理考试,估计 同学的物理分数(精确到个位);
同学的物理分数(精确到个位);(3)就这次考试而言,学号为16号的
 同学数学与物理哪个学科成绩要好一些?(通常为了比较某个学生不同学科的成绩水平,可按公式
同学数学与物理哪个学科成绩要好一些?(通常为了比较某个学生不同学科的成绩水平,可按公式 统一化成标准分再进行比较,其中
统一化成标准分再进行比较,其中 为学科原始分,
为学科原始分, 为学科平均分,
为学科平均分, 为学科标准差).
为学科标准差). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数/(x
 .
.(1)当
 时,求
时,求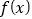 在
在 最小值;
最小值;(2)若
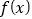 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;(3)求证:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 为奇函数.
为奇函数.(1)求b的值;
(2)证明:函数f(x)在区间(1,+∞)上是减函数;
(3)解关于x的不等式f(1+x2)+f(-x2+2x-4)>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (
( 为参数)与
为参数)与 轴正半轴,
轴正半轴, 轴正半轴的交点分别为
轴正半轴的交点分别为 ,动点
,动点 是椭圆上任一点,则
是椭圆上任一点,则 面积的最大值为( )
面积的最大值为( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

