【题目】下表中的数据是一次阶段性考试某班的数学、物理原始成绩:

用这44人的两科成绩制作如下散点图:

学号为22号的![]() 同学由于严重感冒导致物理考试发挥失常,学号为31号的
同学由于严重感冒导致物理考试发挥失常,学号为31号的![]() 同学因故未能参加物理学科的考试,为了使分析结果更客观准确,老师将
同学因故未能参加物理学科的考试,为了使分析结果更客观准确,老师将![]() 两同学的成绩(对应于图中
两同学的成绩(对应于图中![]() 两点)剔除后,用剩下的42个同学的数据作分析,计算得到下列统计指标:
两点)剔除后,用剩下的42个同学的数据作分析,计算得到下列统计指标:
数学学科平均分为110.5,标准差为18.36,物理学科的平均分为74,标准差为11.18,数学成绩![]()
与物理成绩![]() 的相关系数为
的相关系数为![]() ,回归直线
,回归直线![]() (如图所示)的方程为
(如图所示)的方程为![]() .
.
(1)若不剔除![]() 两同学的数据,用全部44人的成绩作回归分析,设数学成绩
两同学的数据,用全部44人的成绩作回归分析,设数学成绩![]() 与物理成绩
与物理成绩![]() 的相关系数为
的相关系数为![]() ,回归直线为
,回归直线为![]() ,试分析
,试分析![]() 与
与![]() 的大小关系,并在图中画出回归直线
的大小关系,并在图中画出回归直线![]() 的大致位置;
的大致位置;
(2)如果![]() 同学参加了这次物理考试,估计
同学参加了这次物理考试,估计![]() 同学的物理分数(精确到个位);
同学的物理分数(精确到个位);
(3)就这次考试而言,学号为16号的![]() 同学数学与物理哪个学科成绩要好一些?(通常为了比较某个学生不同学科的成绩水平,可按公式
同学数学与物理哪个学科成绩要好一些?(通常为了比较某个学生不同学科的成绩水平,可按公式![]() 统一化成标准分再进行比较,其中
统一化成标准分再进行比较,其中![]() 为学科原始分,
为学科原始分,![]() 为学科平均分,
为学科平均分,![]() 为学科标准差).
为学科标准差).
参考答案:
【答案】(1)![]() ,理由见解析(2)81(3)
,理由见解析(2)81(3)![]()
【解析】
(1)不剔除![]() 两同学的数据,44个数据会使回归效果变差,从而得到
两同学的数据,44个数据会使回归效果变差,从而得到![]() ,描出回归直线即可;(2)将x=125代入回归直线方程,即可得到答案;(3)利用题目给出的标准分计算公式进行计算即可得到结论.
,描出回归直线即可;(2)将x=125代入回归直线方程,即可得到答案;(3)利用题目给出的标准分计算公式进行计算即可得到结论.
(1)![]() ,
,
说明理由可以是:
①离群点A,B会降低变量间的线性关联程度;
②44个数据点与回归直线![]() 的总偏差更大,回归效果更差,所以相关系数更小;
的总偏差更大,回归效果更差,所以相关系数更小;
③42个数据点与回归直线![]() 的总偏差更小,回归效果更好,所以相关系数更大;
的总偏差更小,回归效果更好,所以相关系数更大;
④42个数据点更加贴近回归直线![]() ;
;
⑤44个数据点与回归直线![]() 更离散,或其他言之有理的理由均可.
更离散,或其他言之有理的理由均可.

要点:直线![]() 斜率须大于0且小于
斜率须大于0且小于![]() 的斜率,具体为止稍有出入没关系,无需说明理由.
的斜率,具体为止稍有出入没关系,无需说明理由.
(2)令![]() ,代入
,代入![]()
得![]()
所以,估计![]() 同学的物理分数大约为
同学的物理分数大约为![]() 分.
分.
(3)由表中知![]() 同学的数学原始分为122,物理原始分为82,
同学的数学原始分为122,物理原始分为82,
数学标准分为![]()
物理标准分为![]()
![]() ,故
,故![]() 同学物理成绩比数学成绩要好一些.
同学物理成绩比数学成绩要好一些.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查我市在校中学生参加体育运动的情况,从中随机抽取了16名男同学和14 名女同学,调查发现,男、女同学中分别有12人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下
 列联表:
列联表: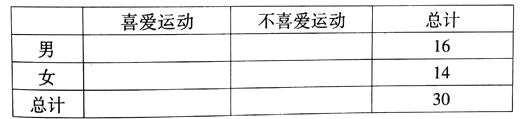
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关?
(3)将以上统计结果中的频率视作概率,从我市中学生中随机抽取3人,若其中喜爱运动的人数为
 ,求
,求 的分布列和均值.
的分布列和均值.参考数据:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 与等比数列
与等比数列 满足
满足 ,
, ,且
,且 .
. (1)求数列
 ,
, 的通项公式;
的通项公式;(2)设
 ,是否存在正整数
,是否存在正整数 ,使
,使 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,
 ,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号


A. 522B. 324C. 535D. 578
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在
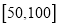 内,发布成绩使用等级制.各等级划分标准见下表.
内,发布成绩使用等级制.各等级划分标准见下表.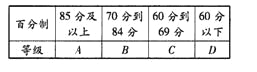
规定:
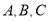 三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了
三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了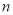 名学生的原始成绩作为样本进行统计.按照
名学生的原始成绩作为样本进行统计.按照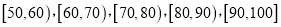 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.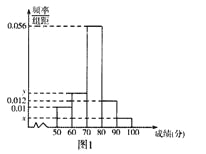
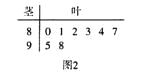
(I)求
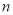 和频率分布直方图中的
和频率分布直方图中的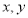 的值,并估计该校高一年级学生成绩是合格等级的概率;
的值,并估计该校高一年级学生成绩是合格等级的概率;(II)在选取的样本中,从
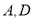 两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是
两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是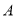 等级的概率.
等级的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数/(x
 .
.(1)当
 时,求
时,求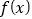 在
在 最小值;
最小值;(2)若
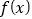 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;(3)求证:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 为奇函数.
为奇函数.(1)求b的值;
(2)证明:函数f(x)在区间(1,+∞)上是减函数;
(3)解关于x的不等式f(1+x2)+f(-x2+2x-4)>0.
相关试题

