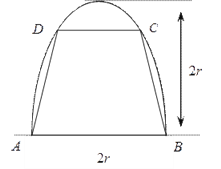
【题目】如图,有一块半椭圆形钢板,其长半轴为![]() ,短半轴为
,短半轴为![]() ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,记
的端点在椭圆上,记![]() ,梯形面积为
,梯形面积为![]() .
.
(Ⅰ)求面积![]() 关于变量
关于变量![]() 的函数表达式,并写出定义域;
的函数表达式,并写出定义域;
(Ⅱ)求面积![]() 的最大值.
的最大值.
参考答案:
【答案】(I)![]()
![]() ,
,
其定义域为![]()
(II)梯形面积![]() 的最大值为
的最大值为![]()
【解析】试题分析:(1)建立平面直角坐标系,得椭圆标准方程,即![]() 满足的方程:
满足的方程:![]() (y≥0),由于
(y≥0),由于![]() ,可解得y=2
,可解得y=2![]() (0<x<r).从而得梯形
(0<x<r).从而得梯形![]() 面积
面积![]() ,其中
,其中![]() ;(2)要求
;(2)要求![]() 最大值,可先求
最大值,可先求![]() 的最大值,这可由导数的知识求得解.
的最大值,这可由导数的知识求得解.
试题解析:(1)依题意,以AB的中点O为原点建立直角坐标系(如图),设点C的横坐标为x.
点C的纵坐标y满足方程![]() (y≥0),
(y≥0),
解得y=2![]() (0<x<r).
(0<x<r).
S=![]() (2x+2r)
(2x+2r)![]() 2
2![]() =2(x+r)·
=2(x+r)·![]() ,
,
其定义域为{x|0<x<r}.
(2)记f(x)=4(x+r)2(r2-x2),0<x<r,
则f ′(x)=8(x+r)2(r-2x).
令f ′(x)=0,则x=![]() r.因为当0<x<
r.因为当0<x<![]() 时,f ′(x)>0;
时,f ′(x)>0;
当![]() <x<r时,f ′(x)<0,所以f(
<x<r时,f ′(x)<0,所以f(![]() r)是f(x)的最大值.
r)是f(x)的最大值.
因此,当x=![]() r时,S取得最大值,最大值为
r时,S取得最大值,最大值为![]() =
=![]() r2,即梯形面积S的最大值为
r2,即梯形面积S的最大值为![]() r2.
r2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
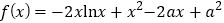 ,记
,记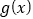 为
为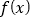 的导函数.
的导函数.(1)若曲线
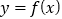 在点
在点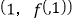 处的切线垂直于直线
处的切线垂直于直线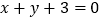 ,求
,求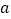 的值;
的值;(2)讨论
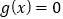 的解的个数;
的解的个数;(3)证明:对任意的
 ,恒有
,恒有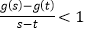 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
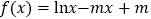 .
.(I)求函数
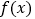 的单调区间;
的单调区间;(II)若
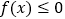 在
在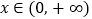 上恒成立,求实数
上恒成立,求实数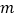 的取值范围;
的取值范围;(III)在(II)的条件下,对任意的
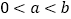 ,求证:
,求证: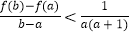 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函
 数是奇函数,且f(2)=
数是奇函数,且f(2)= .
.(1)求实数m和n的值;
(2)求函数f(x)在区间[-2,-1]上的最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
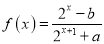 是
是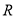 的奇函数,
的奇函数, 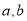 是常数.
是常数.(1)求
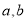 的值;
的值;(2)用定义法证明
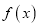 是
是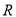 的增函数;
的增函数;(3)不等式
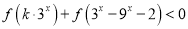 对任意
对任意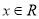 恒成立,求实数
恒成立,求实数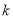 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
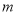 是实数,
是实数,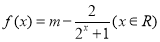 ,
,(1)若函数
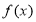 为奇函数,求
为奇函数,求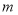 的值;
的值;(2)试用定义证明:对于任意
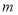 ,
,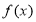 在
在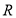 上为单调递增函数;
上为单调递增函数;(3)若函数
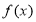 为奇函数,且不等式
为奇函数,且不等式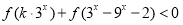 对任意
对任意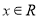 恒成立,求实数
恒成立,求实数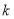 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间20名工人年龄数据如下表:
年龄(岁)
19
24
26
30
34
35
40
合计
工人数(人)
1
3
3
5
4
3
1
20
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
相关试题

