【题目】函数![]() 是
是![]() 的奇函数,
的奇函数, ![]() 是常数.
是常数.
(1)求![]() 的值;
的值;
(2)用定义法证明![]() 是
是![]() 的增函数;
的增函数;
(3)不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:根据函数为奇函数,则f(-x)=-f(x),可直接利用f(-1)=f(1),f(0)=0解出a,b的值,利用定义法证明函数的单调性,证明步骤为:①取值②作差③变形断号④给出结论;根据函数的单调性解不等式,解决恒成立的基本方法就是分离参数利用“极值原理”求出参数的取值范围.
试题解析:
(1)![]()
![]() 是
是![]() 上的奇函数
上的奇函数 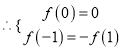
![]()
![]() .
.
(2)设![]() ,且
,且![]() ,则
,则
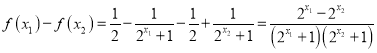
![]()
![]() 又
又![]()
![]() 即
即![]()
![]() 是
是![]() 上的增函数
上的增函数
(3)由题意得: ![]() 对任意
对任意![]() 恒成立
恒成立
又![]() 是
是![]() 上的增函数
上的增函数
![]() 即
即![]() 对任意
对任意![]() 恒成立
恒成立
令![]() 即
即![]() 对
对![]() 恒成立
恒成立
令![]() 对称轴为
对称轴为![]()
当![]() 即
即![]() 时,
时, ![]() 在
在![]() 为增函数,
为增函数, ![]() 成立
成立
![]() 符合
符合
当![]() 即
即![]() 时,
时, ![]() 在
在![]() 为减,
为减, ![]() 为增
为增
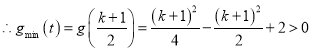
解得![]()
![]()
综上 ![]()
【点精】利用函数的奇偶性,求函数的解析式 ,当函数为奇函数时,则f(-x)=-f(x),可直接利用f(-1)=f(1),f(0)=0解出a,b的值,当函数为偶函数时,利用f(-x)=f(x)求出参数,利用定义法证明函数的单调性,证明步骤为:①取值②作差③变形断号④给出结论;根据函数的单调性解不等式,解决恒成立的基本方法就是分离参数利用“极值原理”求出参数的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
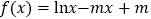 .
.(I)求函数
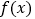 的单调区间;
的单调区间;(II)若
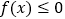 在
在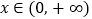 上恒成立,求实数
上恒成立,求实数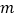 的取值范围;
的取值范围;(III)在(II)的条件下,对任意的
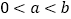 ,求证:
,求证: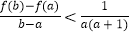 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函
 数是奇函数,且f(2)=
数是奇函数,且f(2)= .
.(1)求实数m和n的值;
(2)求函数f(x)在区间[-2,-1]上的最值.
-
科目: 来源: 题型:
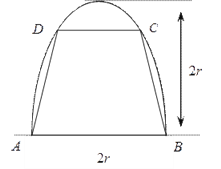
查看答案和解析>>【题目】如图,有一块半椭圆形钢板,其长半轴为
 ,短半轴为
,短半轴为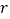 ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底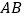 是半椭圆的短轴,上底
是半椭圆的短轴,上底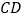 的端点在椭圆上,记
的端点在椭圆上,记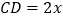 ,梯形面积为
,梯形面积为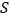 .
.
(Ⅰ)求面积
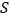 关于变量
关于变量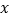 的函数表达式,并写出定义域;
的函数表达式,并写出定义域;(Ⅱ)求面积
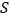 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
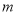 是实数,
是实数,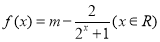 ,
,(1)若函数
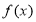 为奇函数,求
为奇函数,求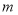 的值;
的值;(2)试用定义证明:对于任意
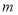 ,
,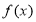 在
在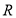 上为单调递增函数;
上为单调递增函数;(3)若函数
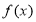 为奇函数,且不等式
为奇函数,且不等式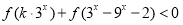 对任意
对任意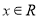 恒成立,求实数
恒成立,求实数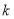 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间20名工人年龄数据如下表:
年龄(岁)
19
24
26
30
34
35
40
合计
工人数(人)
1
3
3
5
4
3
1
20
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对
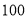 名出租车司机进行调查,调查问卷共
名出租车司机进行调查,调查问卷共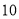 道题,答题情况如下表:
道题,答题情况如下表:答对题目数
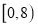
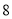
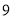
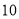
女
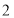
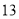
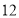
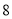
男
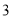
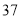
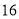
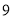
(I)如果出租车司机答对题目大于等于
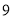 ,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;(II)从答对题目数小于
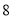 的出租车司机中选出
的出租车司机中选出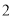 人做进一步的调查,求选出的
人做进一步的调查,求选出的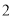 人中至少有一名女出租车司机的概率.
人中至少有一名女出租车司机的概率.
相关试题

