【题目】在直三棱柱![]() 中,
中, ![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积(锥体的体积公式
的体积(锥体的体积公式![]() ,其中
,其中![]() 为底面面积,
为底面面积, ![]() 为高)
为高)
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)欲证![]() 平面
平面![]() ,即证MN∥AC′;(2)利用VA′﹣MNC=VN﹣A′MC=
,即证MN∥AC′;(2)利用VA′﹣MNC=VN﹣A′MC=![]() VN﹣A′BC=
VN﹣A′BC=![]() VA′﹣NBC,求三棱锥A′﹣MNC的体积.
VA′﹣NBC,求三棱锥A′﹣MNC的体积.
试题解析:
(1)
连接AB′,AC′,由已知∠BAC=90°,AB=AC,三棱柱ABC-A′B′C′为直三棱柱,
所以M为AB′的中点,又因为N为B′C′中点,所以MN∥AC′,
又MN平面A′ACC′,AC′平面A′ACC′,所以MN∥平面A′ACC′;
(2)连结BN,由题意A′N⊥B′C′,
∵平面A′B′C′∩平面B′BCC′=B′C′,
∴A′N⊥平面NBC
又A′N=![]() B′C′=1,
B′C′=1,
故VA′﹣MNC=VN﹣A′MC=![]() VN﹣A′BC=
VN﹣A′BC=![]() VA′﹣NBC=
VA′﹣NBC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).

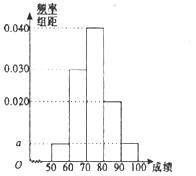
(1)求图中
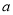 的值;
的值;(2)估计该次考试的平均分
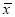 (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);(3)根据已知条件完成下面
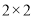 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关? (参考公式:
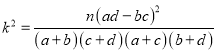 ,其中
,其中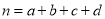 )
)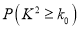
0.40
0.25
0.15
0.10
0.05
0.025
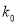
0.780
1.323
2.072
2.706
3.841
5.024
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥的三组相对棱(相对的棱是指三棱锥中成异面直线的一组棱)分别相等,且长分别为
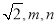 ,其中
,其中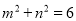 ,则该三棱锥体积的最大值为
,则该三棱锥体积的最大值为A.
 B.
B. 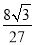 C.
C. 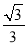 D.
D. 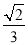
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心在直线上
 ,且与直线
,且与直线 相切于点
相切于点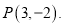
(1)求圆C的方程;
(2)是否存在过点
 的直线
的直线 与圆C交于
与圆C交于 两点,且
两点,且 的面积为
的面积为 (O为坐标原点),若存在,求出直线
(O为坐标原点),若存在,求出直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
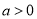 ,且
,且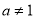 .设
.设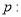 函数
函数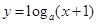 在区间
在区间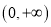 内单调递减;
内单调递减; 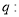 曲线
曲线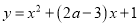 与
与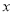 轴交于不同的两点,如果“
轴交于不同的两点,如果“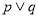 ”为真命题,“
”为真命题,“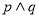 ”为假命题,求实数
”为假命题,求实数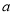 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在等腰梯形
 中,
中,  .把
.把 沿
沿 折起,使得
折起,使得 ,得到四棱锥
,得到四棱锥 .如图2所示.
.如图2所示.
(1)求证:面
 面
面 ;
;(2)求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的长轴长为6,且椭圆
的长轴长为6,且椭圆 与圆
与圆 :
:  的公共弦长为
的公共弦长为 .
.(1)求椭圆
 的方程.
的方程.(2)过点
 作斜率为
作斜率为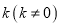 的直线
的直线 与椭圆
与椭圆 交于两点
交于两点 ,
,  ,试判断在
,试判断在 轴上是否存在点
轴上是否存在点 ,使得
,使得 为以
为以 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由.
相关试题

