搜索
【题目】已知奇函数f（x）在（﹣∞，0）上单调递减，且f（2）=0，则不等式（x﹣1）f（x﹣1）＞0的解集是（ ）
A.（﹣3，﹣1）
B.（﹣1，1）∪（1，3）
C.（﹣3，0）∪（3，+∞）
D.（﹣3，1）∪（2，+∞）
参考答案：
【答案】B
【解析】解：∵奇函数f（x）在（﹣∞，0）上单调递减，且f（2）=0，
∴奇函数f（x）在（0，+∞）上单调递减，且f（﹣2）=0，
不等式（x﹣1）f（x﹣1）＞0等价于x﹣1＞0，f（x﹣1）＞0或x﹣1＜0，f（x﹣1）＜0
即 
或 
∴1＜x＜3或﹣1＜x＜1
∴不等式（x﹣1）f（x﹣1）＞0的解集是（﹣1，1）∪（1，3）
故选B．
先确定奇函数f（x）在（0，+∞）上单调递减，且f（﹣2）=0，再将不等式（x﹣1）f（x﹣1）＞0等价于x﹣1＞0，f（x﹣1）＞0或x﹣1＜0，f（x﹣1）＜0，即可求得结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，我国PM2.5标准采用世卫组织设定的最宽限值，即PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米~75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标.某市环保局从市区2017年上半年每天的PM2.5监测数据中随机抽取15天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）
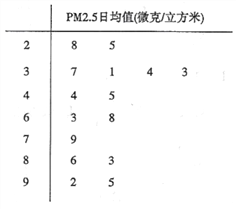
（1）从这15天的数据中任取一天，求这天空气质量达到一级的概率；
（2）从这15天的数据中任取3天的数据，记
表示其中空气质量达到一级的天数，求的分布列；（3）以这15天的PM2.5的日均值来估计一年的空气质量情况，（一年按360天来计算），则一年中大约有多少天的空气质量达到一级.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=loga（1+x），g（x）=loga（1﹣x），其中（a＞0且a≠1），设h（x）=f（x）﹣g（x）．
（1）求h（x）的定义域；
（2）判断h（x）的奇偶性，并说明理由；
（3）若a=log327+log2，求使f（x）＞1成立的x的集合． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中是假命题的是( )
A.?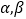
∈R，使sin(
)＝
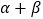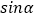＋sinβ
B.?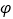
∈R，函数f(x)＝sin(
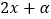)都不是偶函数
C.?m∈R，使f(x)＝(m-1)·m2－4m＋3是幂函数，且在(0，＋∞)上单调递减
D.?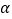
＞0，函数f(x)＝ln2x＋lnx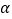－有零点 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列语句:
①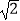
是无限循环小数；②x2-3x+2=0；③当x=4时,2x>0;
④垂直于同一条直线的两条直线必平行吗?⑤一个数不是合数就是质数；
⑥作△ABC≌△A'B'C'；⑦二次函数的图像太美了!
⑧4是集合{1,2,3}中的元素.
其中不是命题的有,是真命题的有.(只填序号) -
科目： 来源： 题型：
查看答案和解析>>【题目】已知定义在
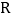上的奇函数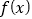
，设其导函数为
，当
时，恒有
，令
，则满足
的实数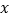
的取值范围是（ ）A.
B. 
C. 
D.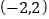 
-
科目： 来源： 题型：
查看答案和解析>>【题目】欧巴老师布置给时镇同学这样一份数学作业：在同一个直角坐标系中画出四个对数函数的图象，使它们的底数分别为
和 
．时镇同学为了和暮烟同学出去玩，问大英同学借了作业本很快就抄好了，详见如图．第二天，欧巴老师当堂质问时镇同学：“你画的四条曲线中，哪条是底数为e的对数函数图象？”时镇同学无言以对，憋得满脸通红，眼看时镇同学就要被欧巴老师训斥一番，聪明睿智的你能不能帮他一把，回答这个问题呢？曲线才是底数为e的对数函数的图象． 
相关试题
