【题目】函数f(x)=|x+1|﹣|2﹣x|.
(1)解不等式f(x)<0;
(2)若m,n∈R+ , ![]() ,求证:n+2m﹣f(x)>0恒成立.
,求证:n+2m﹣f(x)>0恒成立.
参考答案:
【答案】
(1)
解:由f(x)<0得f(x)=|x+1|﹣|2﹣x|<0,即|x+1|<|x﹣2|,
平方得x2+2x+1<x2﹣4x+4,即6x<3,
得x< ![]() ,即不等式的解集为(﹣∞,
,即不等式的解集为(﹣∞, ![]() ).
).
(2)
解:∵n+2m+2=n+1+2m+1=(n+1+2m+1)( ![]() +
+ ![]() )=4+1+
)=4+1+ ![]() +
+ ![]() ≥5+2
≥5+2 ![]() =5+4=9,
=5+4=9,
∴n+2m≥9﹣2=7,当且仅当+ ![]() =
= ![]() ,即n+1=2(2m+1)时取等号,
,即n+1=2(2m+1)时取等号,
∴n+2m的最小值为7,
∵f(x)=|x+1|﹣|2﹣x|≤|x+1+2﹣x|=3,
∴f(x)的最大值为3,
则n+2m>f(x)恒成立,即n+2m﹣f(x)>0恒成立.
【解析】(1)根据绝对值不等式的解法进行求解即可.(2)根据基本不等式的性质,利用1的代换,先求出n+2m的最小值,利用绝对值不等式的性质求出f(x)的最大值,进行比较即可.
【考点精析】掌握基本不等式是解答本题的根本,需要知道基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),直线l的参数方程为
 (t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)已知|PM|,|MN|,|PN|成等比数列,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
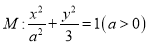 的一个焦点为
的一个焦点为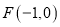 ,左、右顶点分别为
,左、右顶点分别为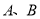 ,经过点
,经过点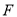 且斜率为
且斜率为 的直线
的直线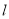 与椭圆
与椭圆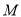 交于
交于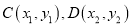 两点.
两点.(1)求椭圆
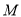 的方程;
的方程;(2)记
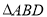 与
与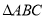 的面积分别为
的面积分别为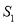 和
和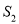 ,求
,求 关于
关于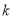 的表达式,并求出当
的表达式,并求出当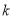 为何值时
为何值时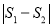 有最大值.
有最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的发展,移动支付
 又称手机支付
又称手机支付 逐渐深入人民群众的生活
逐渐深入人民群众的生活 某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对
某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对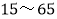 岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表
岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表 部分数据模糊不清
部分数据模糊不清 如表:
如表:分组
频数
频率
第1组
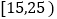
10

第2组
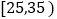

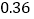
第3组
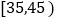
15
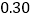
第4组
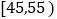


第5组
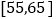
2
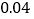
合计
50

 表中
表中 处的数据分别是多少?
处的数据分别是多少? 从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数. 在
在 抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的多面体中,
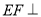 平面
平面
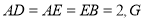 是
是 的中点.
的中点.
(1)求证:
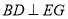 ;
;(2)求二面角
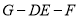 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=
 (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为  ,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )
,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( ) 
A.6平方米
B.9平方米
C.12平方米
D.15平方米 -
科目: 来源: 题型:
查看答案和解析>>【题目】贵阳与凯里两地相距约200千米,一辆货车从贵阳匀速行驶到凯里,规定速度不得超过100千米
 时,已知货车每小时的运输成本
时,已知货车每小时的运输成本 以元为单位
以元为单位 由可变部分和固定部分组成:可变部分与速度
由可变部分和固定部分组成:可变部分与速度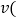 千米
千米 时
时 的平方成正比,比例系数为
的平方成正比,比例系数为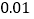 ;固定部分为64元.
;固定部分为64元. 把全程运输成本
把全程运输成本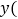 元
元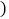 表示为速度
表示为速度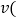 千米
千米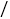 时
时 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域; 为了使全程运输成本最小,货车应以多大速度行驶?
为了使全程运输成本最小,货车应以多大速度行驶?
相关试题

