【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),直线l的参数方程为  (t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)已知|PM|,|MN|,|PN|成等比数列,求a的值.
参考答案:
【答案】
(1)解:曲线C:ρsin2θ=2acosθ(a>0),即ρ2sin2θ=2aρcosθ(a>0),可得直角坐标方程:y2=2ax(a>0).
直线l的参数方程为 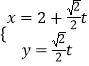 (t为参数),化为普通方程:y=x﹣2
(t为参数),化为普通方程:y=x﹣2
(2)解:点P(﹣2,﹣4)在直线l上,可得直线l的标准方程:  ,代入抛物线方程可得:m2﹣
,代入抛物线方程可得:m2﹣ ![]() m+4a+32=0,
m+4a+32=0,
△= ![]() ﹣4(4a+32)=2a2+16a>0,(a>0).
﹣4(4a+32)=2a2+16a>0,(a>0).
∴m1+m2= ![]() ,m1m2=4a+32.
,m1m2=4a+32.
|PM|=m1,|PN|=m2,|MN|=|m1﹣m2|= ![]() =
= ![]() =
= ![]() .
.
∵|PM|,|MN|,|PN|成等比数列,
∴|MN|2=|PM||PN|,
∴2a2+16a=m1m2=4a+32,化为:a2+6a﹣16=0,a>0,
解得a=2.
【解析】(1)曲线C:ρsin2θ=2acosθ(a>0),即ρ2sin2θ=2aρcosθ(a>0),把x=ρcosθ,y=ρsinθ代入即可得出直角坐标方程.直线l的参数方程为 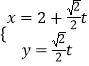 (t为参数),消去参数t化为普通方程:y=x﹣2.(2)点P(﹣2,﹣4)在直线l上,可得直线l的标准方程:
(t为参数),消去参数t化为普通方程:y=x﹣2.(2)点P(﹣2,﹣4)在直线l上,可得直线l的标准方程:  ,代入抛物线方程可得:m2﹣
,代入抛物线方程可得:m2﹣ ![]() m+4a+32=0,|PM|=m1 , |PN|=m2 , |MN|=|m1﹣m2|=
m+4a+32=0,|PM|=m1 , |PN|=m2 , |MN|=|m1﹣m2|= ![]() ,由于|PM|,|MN|,|PN|成等比数列,可得|MN|2=|PM||PN|,即可得出.
,由于|PM|,|MN|,|PN|成等比数列,可得|MN|2=|PM||PN|,即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高级中学在今年“五一”期间给校内所有教室安装了同一型号的空调,关于这批空调的使用年限
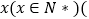 单位:年
单位:年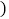 和所支出的维护费用
和所支出的维护费用 单位:千元
单位:千元 厂家提供的统计资料如表:
厂家提供的统计资料如表:x
2
4
5
6
8
y
30
40
60
50
70
 若x与y之间是线性相关关系,请求出维护费用y关于x的线性回归直线方程
若x与y之间是线性相关关系,请求出维护费用y关于x的线性回归直线方程 ;
;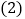 若规定当维护费用y超过
若规定当维护费用y超过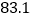 千元时,该批空调必须报度,试根据
千元时,该批空调必须报度,试根据 的结论求该批空调使用年限的最大值
的结论求该批空调使用年限的最大值 结果取整数
结果取整数 参考公式:
参考公式: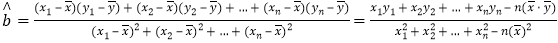 ,
,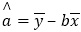 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆O是△ABC的外接圆,∠BAC的平分线交BC于点F,D是AF的延长线与⊙O的交点,AC的延线与⊙O的切线DE交于点E.
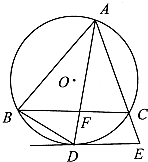
(1)求证: =
= 
(2)若BD=3 ,EC=2,CA=6,求BF的值.
,EC=2,CA=6,求BF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某体校为了备战明年四月份省划艇单人双桨比赛,对本校甲、乙两名划艇运动员在相同条件下进行了6次测试,测得他们划艇最大速度
 单位:
单位: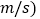 数据如下:
数据如下:甲:27,38,30,37,35,31;
乙:33,29,38,34,28,36.
 试用茎叶图表示甲、乙两名运动员测试的成绩;
试用茎叶图表示甲、乙两名运动员测试的成绩; 根据测试的成绩,你认为派哪名运动员参加明年四月份的省划艇单人双桨比赛比较合适?并说明你的理由
根据测试的成绩,你认为派哪名运动员参加明年四月份的省划艇单人双桨比赛比较合适?并说明你的理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
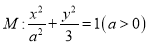 的一个焦点为
的一个焦点为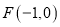 ,左、右顶点分别为
,左、右顶点分别为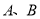 ,经过点
,经过点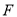 且斜率为
且斜率为 的直线
的直线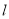 与椭圆
与椭圆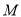 交于
交于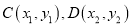 两点.
两点.(1)求椭圆
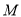 的方程;
的方程;(2)记
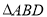 与
与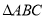 的面积分别为
的面积分别为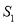 和
和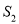 ,求
,求 关于
关于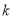 的表达式,并求出当
的表达式,并求出当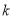 为何值时
为何值时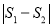 有最大值.
有最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的发展,移动支付
 又称手机支付
又称手机支付 逐渐深入人民群众的生活
逐渐深入人民群众的生活 某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对
某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对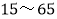 岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表
岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表 部分数据模糊不清
部分数据模糊不清 如表:
如表:分组
频数
频率
第1组
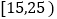
10

第2组
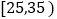

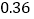
第3组
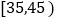
15
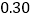
第4组
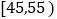


第5组
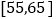
2
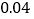
合计
50

 表中
表中 处的数据分别是多少?
处的数据分别是多少? 从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数. 在
在 抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=|x+1|﹣|2﹣x|.
(1)解不等式f(x)<0;
(2)若m,n∈R+ , ,求证:n+2m﹣f(x)>0恒成立.
,求证:n+2m﹣f(x)>0恒成立.
相关试题

