【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(cosα,sinα),设
=(cosα,sinα),设 ![]() =
= ![]() ﹣t
﹣t ![]() (t为实数).
(t为实数).
(1)t=1 时,若 ![]() ∥
∥ ![]() ,求2cos2α﹣sin2α的值;
,求2cos2α﹣sin2α的值;
(2)若α= ![]() ,求|
,求| ![]() |的最小值,并求出此时向量
|的最小值,并求出此时向量 ![]() 在
在 ![]() 方向上的投影.
方向上的投影.
参考答案:
【答案】
(1)解:t=1, ![]() =
= ![]() ﹣t
﹣t ![]() =(1﹣cosα,2﹣sinα).
=(1﹣cosα,2﹣sinα).
∵ ![]() ∥
∥ ![]() ,
,
∴cosα(1﹣sinα)﹣sinα(1﹣cosα)=0,
∴tanα=2;
∴2cos2α﹣sin2α= ![]() =
= ![]() =﹣
=﹣ ![]()
(2)解:α= ![]() ,|
,| ![]() |=
|= ![]() =
= ![]() =
= ![]() ,
,
当t= ![]() 时,
时, ![]() =
= ![]() .
.
当t= ![]() 时,
时, ![]() 时,
时,
![]() =
= ![]() ﹣
﹣ ![]()
![]() =(1,2)﹣
=(1,2)﹣ ![]() =
= ![]() .
.
∴向量 ![]() 在
在 ![]() 方向上的投影
方向上的投影 ![]() =
= 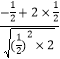 =
= ![]()
【解析】(1)利用向量共线定理可得tanα,再利用同角三角函数基本关系式即可得出;(2)利用向量模的计算公式、二次函数的单调性、向量投影计算公式即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
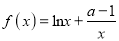 ,
, 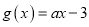 (
(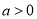 ).
).(1)求函数
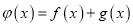 的单调增区间;
的单调增区间;(2)当
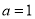 时,记
时,记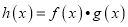 ,是否存在整数
,是否存在整数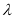 ,使得关于
,使得关于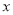 的不等式
的不等式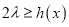 有解?若存在,请求出
有解?若存在,请求出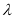 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于数列{an},定义
 为{an}的“优值”,现在已知某数列{an}的“优值”
为{an}的“优值”,现在已知某数列{an}的“优值”  ,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 .
,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面内一动点
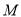 与两定点
与两定点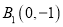 和
和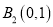 连线的斜率之积等于
连线的斜率之积等于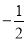 .
.(Ⅰ)求动点
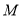 的轨迹
的轨迹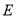 的方程;
的方程;(Ⅱ)设直线
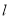 :
: 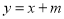 (
( )与轨迹
)与轨迹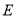 交于
交于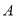 、
、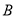 两点,线段
两点,线段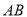 的垂直平分线交
的垂直平分线交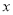 轴于点
轴于点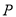 ,当
,当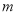 变化时,求
变化时,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
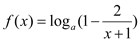 (
(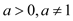 ).
).(1)写出函数
 的值域,单调区间(不必证明);
的值域,单调区间(不必证明);(2)是否存在实数
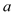 使得
使得 的定义域为
的定义域为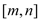 ,值域为
,值域为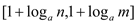 ?若存在,求出实数
?若存在,求出实数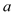 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组
 ,第二组
,第二组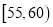 ,…,第五组
,…,第五组 ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为 .
.
(Ⅰ)求
 的值,并求这50名同学心率的平均值;
的值,并求这50名同学心率的平均值;(Ⅱ)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?说明你的理由.
参考数据:

0.15
0.10
0.05
0.025
0.010
0.005
0.001
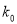
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:
 ,其中
,其中
心率小于60次/分
心率不小于60次/分
合计
体育生
20
艺术生
30
合计
50
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
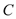 的圆心在直线
的圆心在直线 上,且与直线
上,且与直线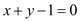 相切于点
相切于点 .
.(1)求圆
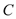 方程;
方程;(2)是否存在过点
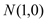 的直线
的直线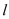 与圆
与圆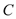 交于
交于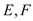 两点,且
两点,且 的面积是
的面积是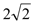 (
(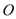 为坐标原点),若存在,求出直线
为坐标原点),若存在,求出直线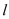 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
相关试题

