【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
参考答案:
【答案】(1)当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ;
; ![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ;(2)0.
;(2)0.
【解析】试题分析:(Ⅰ)先求函数的导函数,原函数的单调增区间即为使导函数大于零的区间,根据导函数分段讨论![]() 的不同取值范围时的单调增区间即可.
的不同取值范围时的单调增区间即可.
(Ⅱ)![]() 单调递增,存在唯一
单调递增,存在唯一![]() ,使得
,使得![]() ,即
,即![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]()
![]() 求得
求得![]() 的范围,得到
的范围,得到![]() 的范围,得到
的范围,得到![]() 最小整数值.
最小整数值.
试题解析:(1)![]() (
(![]() )
)
①当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
②当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
③当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
综上所述,
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ;
;
![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() .
.
(2)当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 单调递增,
单调递增, ![]() ,
, ![]() ,
,
所以存在唯一![]() ,使得
,使得![]() ,即
,即![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以![]()
 ,
,
记函数![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,
,
由![]() ,且
,且![]() 为整数,得
为整数,得![]() ,
,
所以存在整数![]() 满足题意,且
满足题意,且![]() 的最小值为0.
的最小值为0.
点晴:本题主要考查导数的单调性,导数与极值点、不等式等知识. 解答此类问题,应该首先确定函数的定义域,否则,写出的单调区间易出错. 解决含参数问题及不等式问题注意两个转化:(1)利用导数解决含有参数的单调性问题可将问题转化为不等式恒成立问题,要注意分类讨论和数形结合思想的应用.(2)将不等式的证明、方程根的个数的判定转化为函数的单调性问题处理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙丙丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为
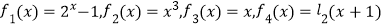 , 有以下结论:
, 有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当0<x<1时,丁在最前面,当x>1时,丁在最后面;
④丙不可能在最前面,也不可能最最后面;
⑤如果它们已知运动下去,最终在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隔河看两目标A、B,但不能到达,在岸边选取相距
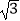 km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离. 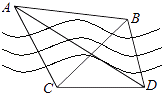
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,三棱柱
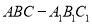 中,侧面
中,侧面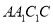
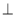 底面
底面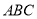 ,
, 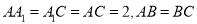 ,且
,且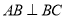 ,O为
,O为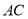 中点.
中点.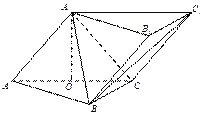
(Ⅰ)证明:
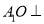 平面
平面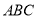 ;
;(Ⅱ)求直线
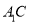 与平面
与平面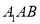 所成角的正弦;
所成角的正弦;(Ⅲ)在
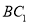 上是否存在一点
上是否存在一点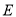 ,使得
,使得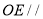 平面
平面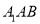 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点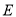 的位置.
的位置. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于数列{an},定义
 为{an}的“优值”,现在已知某数列{an}的“优值”
为{an}的“优值”,现在已知某数列{an}的“优值”  ,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 .
,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面内一动点
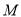 与两定点
与两定点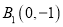 和
和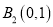 连线的斜率之积等于
连线的斜率之积等于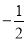 .
.(Ⅰ)求动点
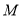 的轨迹
的轨迹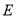 的方程;
的方程;(Ⅱ)设直线
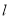 :
: 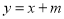 (
( )与轨迹
)与轨迹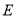 交于
交于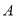 、
、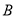 两点,线段
两点,线段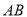 的垂直平分线交
的垂直平分线交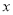 轴于点
轴于点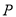 ,当
,当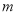 变化时,求
变化时,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
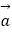 =(1,2),
=(1,2), 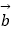 =(cosα,sinα),设
=(cosα,sinα),设 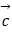 =
= 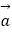 ﹣t
﹣t 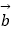 (t为实数).
(t为实数).
(1)t=1 时,若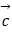 ∥
∥ 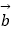 ,求2cos2α﹣sin2α的值;
,求2cos2α﹣sin2α的值;
(2)若α= ,求|
,求| 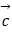 |的最小值,并求出此时向量
|的最小值,并求出此时向量 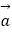 在
在 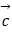 方向上的投影.
方向上的投影.
相关试题

