【题目】以边长为4的等比三角形![]() 的顶点
的顶点![]() 以及
以及![]() 边的中点
边的中点![]() 为左、右焦点的椭圆过
为左、右焦点的椭圆过![]() 两点.
两点.
(1)求该椭圆的标准方程;
(2)过点![]() 且
且![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() 两点,求证直线
两点,求证直线![]() 与
与![]() 的交点在一条直线上.
的交点在一条直线上.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)先建立直角坐标系,使椭圆方程为标准方程,则![]()
(2)研究圆锥曲线的定值问题,一般方法为以算代证,即先求两直线交点坐标,再确定交点所在定直线:由对称性可知两直线交点必在垂直于x轴的直线上,因此运算目标为求交点横坐标为定值,设![]() 的方程为
的方程为![]() ,
, ![]() ,则
,则![]() :
: ![]() ,
, ![]() :
: ![]() ,消去y得
,消去y得![]() ,再利用直线方程与椭圆方程联立方程组,结合韦达定理可得
,再利用直线方程与椭圆方程联立方程组,结合韦达定理可得![]() ,
, ![]() ,代入化简得
,代入化简得![]()
试题解析:(1) 由题意可知两焦点为![]() 与
与![]() ,且
,且![]() ,因此椭圆的方程为
,因此椭圆的方程为![]() . (4分)
. (4分)
(2) ① 当![]() 不与
不与![]() 轴重合时,
轴重合时,
设![]() 的方程为
的方程为![]() ,且
,且![]() ,
, ![]()
联立椭圆与直线![]()
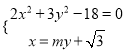 消去
消去![]() 可得
可得![]() ,即
,即![]() ,
, ![]()
设![]() ,
, ![]()
则![]() :
: ![]() ①
①
![]() :
: ![]() ②
②
②-①得
![]()
![]()
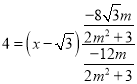
![]()
则![]() ,即
,即![]() .
.
②当![]() 与
与![]() 轴重合时,即
轴重合时,即![]() 的方程为
的方程为![]() ,即
,即![]() ,
, ![]() .
.
即![]() :
: ![]() ①
①
![]() :
: ![]() ②
②
联立①和②消去![]() 可得
可得![]() .
.
综上![]() 与
与![]() 的交点在直线
的交点在直线![]() 上.
上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a|=4,|b|=8,a与b的夹角是120°.
(1) 计算:① |a+b|,② |4a-2b|;
(2) 当k为何值时,(a+2b)⊥(ka-b)? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.若直线l过点A(4,0),且被圆C1截得的弦长为2
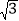 ,求直线l的方程;
,求直线l的方程; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,且满足
 .
.
(1)求证:四边形EFGH是梯形;
(2)若BD=a,求梯形EFGH的中位线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
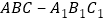 中,
中,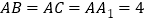 ,
,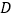 为棱
为棱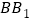 上一点,
上一点,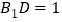 ,
,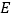 为线段
为线段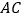 上一点,
上一点,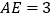 .
.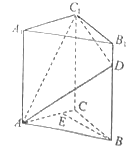
(Ⅰ)证明:
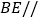 平面
平面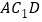 ;
;(Ⅱ)若
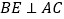 ,求四棱锥
,求四棱锥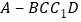 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
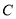 经过
经过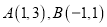 两点,且圆心在直线
两点,且圆心在直线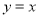 上.
上.(Ⅰ)求圆
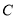 的标准方程;
的标准方程;(Ⅱ)设直线
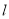 经过点
经过点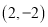 ,且
,且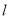 与圆
与圆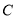 相交所得弦长为
相交所得弦长为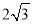 ,求直线
,求直线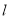 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线
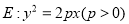 上的点
上的点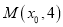 到焦点
到焦点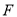 的距离
的距离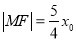 .
.
(Ⅰ)求抛物线
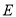 的方程;
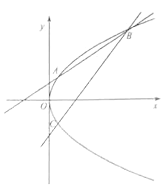
的方程;(Ⅱ)如图,直线
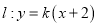 与抛物线
与抛物线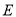 交于
交于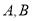 两点,点
两点,点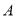 关于
关于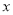 轴的对称点是
轴的对称点是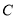 .求证:直线
.求证:直线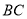 恒过一定点.
恒过一定点.
相关试题

