【题目】在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.若直线l过点A(4,0),且被圆C1截得的弦长为2![]() ,求直线l的方程;
,求直线l的方程;
参考答案:
【答案】y=0或7x+24y-28=0.
【解析】试题分析:根据直线和圆相交的弦长公式设出直线斜率,根据半弦长、半径、弦心距满足勾股定理,解方程求出k值,代入即得直线l的方程.
试题解析:
由题意可知直线l的斜率存在,设直线l的方程为y=k(x-4),即kx-y-4k=0,所以圆心C1(-3,1)到直线l的距离![]() ,由点到直线的距离公式得
,由点到直线的距离公式得![]() =1,化简得24k2+7k=0,解得k=0或k=-
=1,化简得24k2+7k=0,解得k=0或k=-![]() .
.
所以直线l的方程为y=0或y=-![]() (x-4),即y=0或7x+24y-28=0.
(x-4),即y=0或7x+24y-28=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
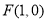 ,直线
,直线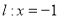 ,动点
,动点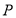 到点
到点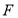 的距离等于它到直线
的距离等于它到直线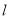 的距离.
的距离.(Ⅰ)求点
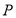 的轨迹
的轨迹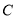 的方程;
的方程;(Ⅱ)是否存在过
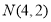 的直线
的直线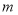 ,使得直线
,使得直线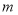 被曲线
被曲线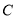 截得的弦
截得的弦 恰好被点
恰好被点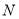 所平分?
所平分? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 椭圆
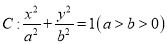 的离心率是
的离心率是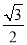 ,点
,点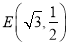 在椭圆上, 设点
在椭圆上, 设点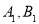 分别是椭圆的右顶点和上顶点, 过 点
分别是椭圆的右顶点和上顶点, 过 点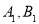 引椭圆
引椭圆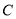 的两条弦
的两条弦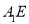 、
、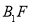 .
.(1)求椭圆
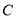 的方程;
的方程;(2)若直线
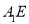 与
与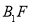 的斜率是互为相反数.
的斜率是互为相反数.①直线
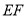 的斜率是否为定值?若是求出该定值, 若不是,说明理由;
的斜率是否为定值?若是求出该定值, 若不是,说明理由;②设
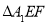 、
、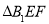 的面积分别为
的面积分别为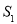 和
和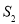 ,求
,求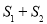 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a|=4,|b|=8,a与b的夹角是120°.
(1) 计算:① |a+b|,② |4a-2b|;
(2) 当k为何值时,(a+2b)⊥(ka-b)? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,且满足
 .
.
(1)求证:四边形EFGH是梯形;
(2)若BD=a,求梯形EFGH的中位线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以边长为4的等比三角形
 的顶点
的顶点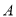 以及
以及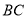 边的中点
边的中点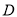 为左、右焦点的椭圆过
为左、右焦点的椭圆过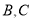 两点.
两点.(1)求该椭圆的标准方程;
(2)过点
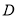 且
且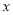 轴不垂直的直线
轴不垂直的直线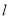 交椭圆于
交椭圆于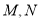 两点,求证直线
两点,求证直线 与
与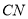 的交点在一条直线上.
的交点在一条直线上. -
科目: 来源: 题型:
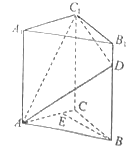
查看答案和解析>>【题目】如图,直三棱柱
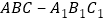 中,
中,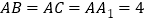 ,
,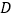 为棱
为棱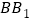 上一点,
上一点,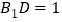 ,
,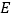 为线段
为线段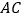 上一点,
上一点,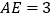 .
.
(Ⅰ)证明:
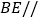 平面
平面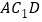 ;
;(Ⅱ)若
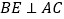 ,求四棱锥
,求四棱锥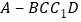 的体积.
的体积.
相关试题

