【题目】已知圆![]() 经过
经过![]() 两点,且圆心在直线
两点,且圆心在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 经过点
经过点![]() ,且
,且![]() 与圆
与圆![]() 相交所得弦长为
相交所得弦长为![]() ,求直线
,求直线![]() 的方程.
的方程.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)求圆的方程,需要三个独立条件,一般设标准式,代入三个条件,解方程组即可;本题也可设成圆的一般式![]() ,再将两个点坐标代入,解方程组可得.(Ⅱ)涉及圆中弦长问题,一般利用垂径定理,即将弦长条件转化为圆心到直线距离,再根据点到直线距离公式求直线斜率,注意验证直线斜率不存在的情形.
,再将两个点坐标代入,解方程组可得.(Ⅱ)涉及圆中弦长问题,一般利用垂径定理,即将弦长条件转化为圆心到直线距离,再根据点到直线距离公式求直线斜率,注意验证直线斜率不存在的情形.
试题解析:解:(Ⅰ)设圆![]() 的圆心坐标为
的圆心坐标为![]() ,
,
依题意,有![]() ,
,
解得![]() ,所以
,所以![]() ,
,
所以圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)依题意,圆![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
(1)若直线![]() 的斜率不存在,则
的斜率不存在,则![]() ,符合题意,此时直线的方程为
,符合题意,此时直线的方程为![]() .
.
(2)若直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,则
,则![]() ,解得
,解得![]() .
.
此时直线![]() 的方程为
的方程为![]()
综上,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,且满足
 .
.
(1)求证:四边形EFGH是梯形;
(2)若BD=a,求梯形EFGH的中位线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以边长为4的等比三角形
 的顶点
的顶点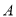 以及
以及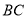 边的中点
边的中点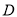 为左、右焦点的椭圆过
为左、右焦点的椭圆过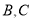 两点.
两点.(1)求该椭圆的标准方程;
(2)过点
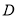 且
且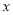 轴不垂直的直线
轴不垂直的直线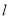 交椭圆于
交椭圆于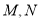 两点,求证直线
两点,求证直线 与
与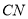 的交点在一条直线上.
的交点在一条直线上. -
科目: 来源: 题型:
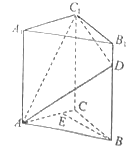
查看答案和解析>>【题目】如图,直三棱柱
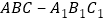 中,
中,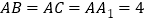 ,
,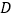 为棱
为棱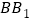 上一点,
上一点,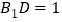 ,
,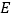 为线段
为线段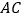 上一点,
上一点,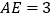 .
.
(Ⅰ)证明:
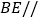 平面
平面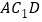 ;
;(Ⅱ)若
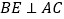 ,求四棱锥
,求四棱锥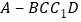 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线
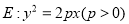 上的点
上的点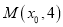 到焦点
到焦点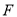 的距离
的距离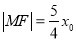 .
.
(Ⅰ)求抛物线
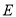 的方程;
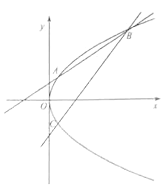
的方程;(Ⅱ)如图,直线
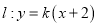 与抛物线
与抛物线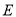 交于
交于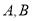 两点,点
两点,点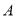 关于
关于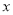 轴的对称点是
轴的对称点是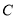 .求证:直线
.求证:直线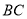 恒过一定点.
恒过一定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙依次有放回地随机抽取1个小球,取到小球的编号分别为
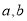 .在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,则甲、乙两人成为“好朋友”的概率为__________.
.在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,则甲、乙两人成为“好朋友”的概率为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程。

相关试题

