【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() 为棱
为棱![]() 上一点,
上一点,![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() .
.
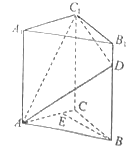
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
参考答案:
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】试题分析:(Ⅰ)证明线面平行,一般方法为利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往结合平几知识,如本题构造平行四边形,利用平行四边形性质得线线平行(Ⅱ)求棱锥的体积,关键是求高,而高的探求实质是利用线面垂直关系,本题可由直三棱柱得侧面与底面垂直,再根据面面垂直性质定理转化为线面垂直,即得锥的高,最后代入锥的体积公式即可.
试题解析:(Ⅰ)证明:如图,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
由![]() ,故
,故![]() ,得
,得![]() .
.
由![]() ,故
,故![]() ,
,
又![]() ,故
,故![]() .
.
所以四边形![]() 为平行四边形,从而
为平行四边形,从而![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.
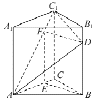
(Ⅱ)解:由已知![]() ,因为
,因为![]() ,
,
则![]() 中,
中,![]() ,
,
![]() 中,
中,![]() .
.
由![]() 知
知![]() 为等腰三角形,设底边
为等腰三角形,设底边![]() 上的高为
上的高为![]() ,
,
则![]() ,
,
![]() ,
,
所以四棱锥![]() 的体积
的体积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.若直线l过点A(4,0),且被圆C1截得的弦长为2
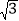 ,求直线l的方程;
,求直线l的方程; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,且满足
 .
.
(1)求证:四边形EFGH是梯形;
(2)若BD=a,求梯形EFGH的中位线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以边长为4的等比三角形
 的顶点
的顶点 以及
以及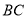 边的中点
边的中点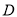 为左、右焦点的椭圆过
为左、右焦点的椭圆过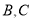 两点.
两点.(1)求该椭圆的标准方程;
(2)过点
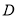 且
且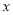 轴不垂直的直线
轴不垂直的直线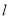 交椭圆于
交椭圆于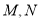 两点,求证直线
两点,求证直线 与
与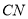 的交点在一条直线上.
的交点在一条直线上. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
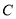 经过
经过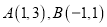 两点,且圆心在直线
两点,且圆心在直线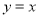 上.
上.(Ⅰ)求圆
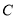 的标准方程;
的标准方程;(Ⅱ)设直线
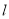 经过点
经过点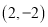 ,且
,且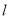 与圆
与圆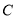 相交所得弦长为
相交所得弦长为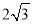 ,求直线
,求直线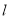 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线
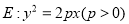 上的点
上的点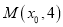 到焦点
到焦点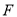 的距离
的距离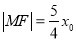 .
.
(Ⅰ)求抛物线
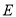 的方程;
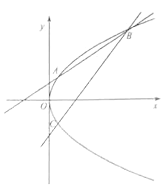
的方程;(Ⅱ)如图,直线
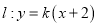 与抛物线
与抛物线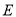 交于
交于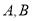 两点,点
两点,点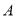 关于
关于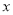 轴的对称点是
轴的对称点是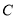 .求证:直线
.求证:直线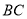 恒过一定点.
恒过一定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙依次有放回地随机抽取1个小球,取到小球的编号分别为
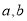 .在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,则甲、乙两人成为“好朋友”的概率为__________.
.在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,则甲、乙两人成为“好朋友”的概率为__________.
相关试题

