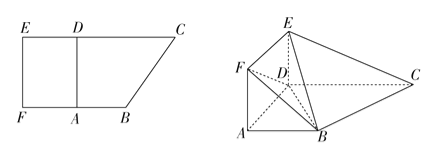
【题目】【2017银川一中模拟】如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
(1)求证:BC⊥平面BDE;
(2)若点D到平面BEC的距离为![]() ,求三棱锥F-BDE的体积.
,求三棱锥F-BDE的体积.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】(1)证明:在矩形ADEF中,ED⊥AD,因为平面ADEF⊥平面ABCD,
所以 ED⊥平面ABCD,所以ED⊥BC. 又在直角梯形ABCD中,
AB=AD=1,CD=2,∠BDC=45°,所以BC=![]() ,
,
在△BCD中,BD=BC=![]() ,CD=2,
,CD=2,
所以BD2+BC2=CD2, 所以BC⊥BD,所以BC⊥平面BDE.
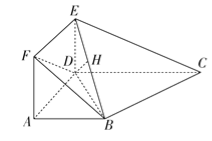
(2)由(1)得,平面DBE⊥平面BCE,作DH⊥BE于点H,
则DH⊥平面BCE,所以DH=![]() .在△BDE中,BD·DE=BE·DH,
.在△BDE中,BD·DE=BE·DH,
即![]() ·DE=
·DE=![]() (
(![]() ),解得DE=1.所以VF-BDE=VB-EFD=
),解得DE=1.所以VF-BDE=VB-EFD=![]() ×
×![]() ×1×1×1=
×1×1×1=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
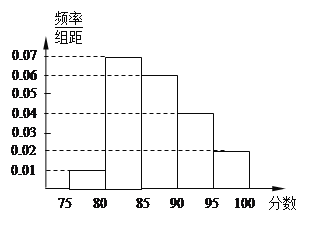
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列5个命题中正确命题的个数是( )
①对于命题p:x∈R,使得x2+x+1<0,则綈p:x∈R,均有x2+x+1>0;
②m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
③已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则线性回归方程为
 =1.23x+0.08;
=1.23x+0.08;④若实数x,y∈[-1,1],则满足x2+y2≥1的概率为
 ;
;⑤曲线y=x2与y=x所围成图形的面积是S= (x-x2)dx.
A.2 B.3
C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分14分)已知函数
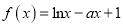 。
。(1)若曲线
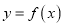 在点
在点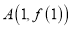 处的切线
处的切线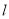 与直线
与直线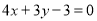 垂直,求实数
垂直,求实数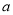 的值;
的值;(2)若
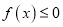 恒成立,求实数
恒成立,求实数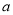 的取值范围;
的取值范围;(3)证明:
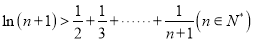
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①将一组数据中的每个数据都乘以同一个非零常数
 后,标准差也变为原来的
后,标准差也变为原来的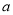 倍;
倍;②设有一个回归方程
 ,变量
,变量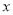 增加1个单位时,
增加1个单位时, 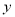 平均减少5个单位;
平均减少5个单位;③线性相关系数
 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;④在某项测量中,测量结果
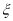 服从正态分布
服从正态分布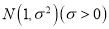 ,若
,若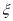 位于区域
位于区域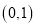 的概率为0.4,则
的概率为0.4,则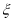 位于区域
位于区域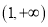 内的概率为0.6
内的概率为0.6⑤利用统计量
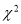 来判断“两个事件
来判断“两个事件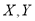 的关系”时,算出的
的关系”时,算出的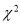 值越大,判断“
值越大,判断“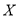 与
与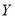 有关”的把握就越大
有关”的把握就越大其中正确的个数是
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求证:
 .
.(2)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①试从上述五个式子中选择一个,求出这个常数;
②根据①的计算结果,将该同学的发现推广为三角恒等式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|x2-3x+2≤0},集合B={y|y=x2-2x+a},集合C={x|x2-ax-4≤0}.命题p:A∩B≠;命题q:AC.
(1)若命题p为假命题,求实数a的取值范围;
(2)若命题p∧q为真命题,求实数a的取值范围.
相关试题

