【题目】下列5个命题中正确命题的个数是( )
①对于命题p:x∈R,使得x2+x+1<0,则綈p:x∈R,均有x2+x+1>0;
②m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
③已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则线性回归方程为![]() =1.23x+0.08;
=1.23x+0.08;
④若实数x,y∈[-1,1],则满足x2+y2≥1的概率为![]() ;
;
⑤曲线y=x2与y=x所围成图形的面积是S= (x-x2)dx.
A.2 B.3
C.4 D.5
参考答案:
【答案】A
【解析】①错,应当是綈p:x∈R,均有x2+x+1≥0;②错,当m=0时,两直线也垂直,所以m=3是两直线垂直的充分不必要条件;③正确,将样本点的中心的坐标代入,满足方程;④错,实数x,y∈[-1,1]表示的平面区域为边长为2的正方形,其面积为4,而x2+y2<1所表示的平面区域的面积为π,所以满足x2+y2≥1的概率为![]() ;⑤正确,由定积分的几何意义可知.
;⑤正确,由定积分的几何意义可知.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
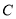 :
: 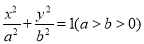 的离心率为
的离心率为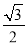 ,以椭圆
,以椭圆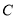 的左顶点
的左顶点 为圆心作圆
为圆心作圆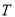 :
: 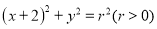 ,设圆
,设圆 与椭圆
与椭圆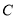 交于点
交于点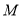 与点
与点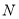 .
.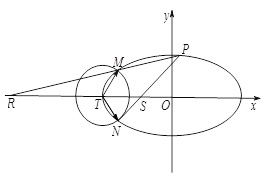
(1)求椭圆
 的方程;
的方程;(2)求
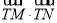 的最小值,并求此时圆
的最小值,并求此时圆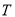 的方程;
的方程;(3)设点
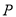 是椭圆
是椭圆 上异于
上异于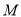 ,
, 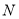 的任意一点,且直线
的任意一点,且直线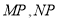 分别与
分别与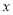 轴交于点
轴交于点 ,
, 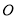 为坐标原点,求证:
为坐标原点,求证: 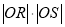 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“开门大吉”是中央电视台推出的娱乐节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌
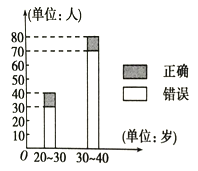
的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1) 完成下列2×2列联表(见答题纸);
(2)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)

0.10
0.05
0.010
0.005
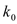
2.706
3.841
6.635
7.879
(参考公式:
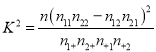 ,
, 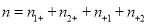 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
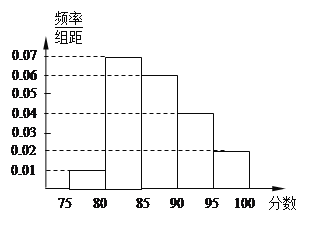
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分14分)已知函数
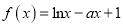 。
。(1)若曲线
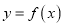 在点
在点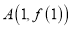 处的切线
处的切线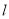 与直线
与直线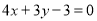 垂直,求实数
垂直,求实数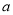 的值;
的值;(2)若
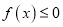 恒成立,求实数
恒成立,求实数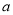 的取值范围;
的取值范围;(3)证明:
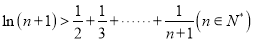
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017银川一中模拟】如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=
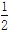 CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.(1)求证:BC⊥平面BDE;
(2)若点D到平面BEC的距离为
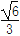 ,求三棱锥F-BDE的体积.
,求三棱锥F-BDE的体积.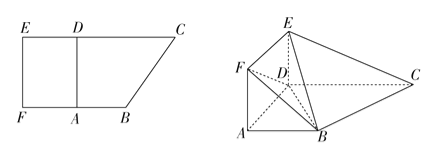
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①将一组数据中的每个数据都乘以同一个非零常数
 后,标准差也变为原来的
后,标准差也变为原来的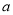 倍;
倍;②设有一个回归方程
 ,变量
,变量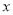 增加1个单位时,
增加1个单位时, 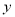 平均减少5个单位;
平均减少5个单位;③线性相关系数
 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;④在某项测量中,测量结果
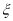 服从正态分布
服从正态分布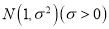 ,若
,若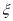 位于区域
位于区域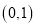 的概率为0.4,则
的概率为0.4,则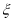 位于区域
位于区域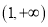 内的概率为0.6
内的概率为0.6⑤利用统计量
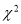 来判断“两个事件
来判断“两个事件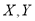 的关系”时,算出的
的关系”时,算出的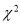 值越大,判断“
值越大,判断“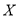 与
与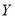 有关”的把握就越大
有关”的把握就越大其中正确的个数是
A. 1 B. 2 C. 3 D. 4
相关试题

