【题目】已知![]() ,
,
(1)求函数![]() 的单调区间;
的单调区间;
(2)若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) 函数在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;(2)
上单调递减;(2) ![]() .
.
【解析】试题分析:
(1)求出导数![]() ,在定义域内,解不等式
,在定义域内,解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;(2)题设不等式可变形为
得减区间;(2)题设不等式可变形为![]() ,分别设
,分别设![]() ,
, ![]() ,求出它们的导数
,求出它们的导数![]() ,通过解相应不等式得出单调区间,求出最值,恰好是
,通过解相应不等式得出单调区间,求出最值,恰好是![]() 时,
时, ![]() 取最小值,
取最小值, ![]() 最最大值,因此要使原不等式恒成立,只要
最最大值,因此要使原不等式恒成立,只要![]() 即可.
即可.
试题解析:
(1)由![]() 得:
得: 
由于定义域为![]() ,
,
所以由![]() 得:
得: ![]()
所以由![]() 得:
得: ![]()
即得函数在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减。
上单调递减。
(2)由不等式![]() 恒成立,
恒成立,
即![]() 恒成立
恒成立
设![]() 得:
得:
![]()
因为它们的定义域![]() ,所以易得:
,所以易得:
函数![]() 在
在![]() 上单调递减,
上单调递减, ![]() 上单调递增;
上单调递增;
函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() 上单调递减;
上单调递减;
这两个函数在![]() 处,
处, ![]() 有最小值,
有最小值, ![]() 有最大值,
有最大值,
所以要使不等式![]() 恒成立,
恒成立,
则只需满足![]() ,即
,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,没有实数根的是( )
A.2x+3=0
B.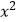 ﹣1=0
﹣1=0
C.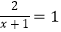
D.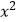 +x+1=0
+x+1=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们对环境关注度的提高,绿色低碳出行越来越受到市民重视. 为此贵阳市建立了公共自行车服务系统,市民凭本人二代身份证到自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20积分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.3.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量
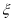 ,求
,求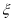 的分布列和数学期望
的分布列和数学期望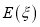 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )

A.5个
B.4个
C.3个
D.2个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是
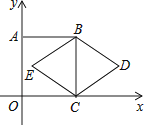
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形
 为直角梯形,
为直角梯形,  ,若
,若 是以
是以 为底边的等腰直角三角形,且
为底边的等腰直角三角形,且 .
.
(1)证明:
 平面
平面 ;
;(2)求直线
 与平面
与平面 所成的角的大小.
所成的角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t≤1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:

(1)此次抽查的学生数为人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人.
相关试题

