【题目】设函数![]() ,
, ![]() 为正实数.
为正实数.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求证: ![]() ;
;
(3)若函数![]() 有且只有
有且只有![]() 个零点,求
个零点,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() (2)详见解析(3)
(2)详见解析(3)![]() .
.
【解析】试题分析:(1)由导数几何意义得![]() ,所以先求导数
,所以先求导数![]() ,代入即得
,代入即得![]() ,又
,又![]() ,由点斜式得切线方程
,由点斜式得切线方程![]() (2)由于
(2)由于![]() ,所以转化为证明
,所以转化为证明![]() 恒成立,即
恒成立,即![]() ,转化为利用导数求函数最值
,转化为利用导数求函数最值![]() (3)因为
(3)因为![]() ,而
,而![]() 先增后减,且
先增后减,且![]() ,所以
,所以![]() 必为最大值(极大值),解得
必为最大值(极大值),解得![]() ,最后证明当1不为极值点时,
,最后证明当1不为极值点时, ![]() 的零点不唯一.
的零点不唯一.
试题解析:(1)当![]() 时,
时, ![]() ,则
,则![]() ,……………2分
,……………2分
所以![]() ,又
,又![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .…………4分
.…………4分
(2)因为![]() ,设函数
,设函数![]() ,
,
则![]() , …………………………………………………6分
, …………………………………………………6分
令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
| 极大值 |
|
所以![]() 的极大值为
的极大值为![]() .
.
所以![]() .………………………………………………8分
.………………………………………………8分
(3)![]() ,
, ![]() ,
,
令![]() ,得
,得![]() ,因为
,因为![]() ,
,
所以![]() 在
在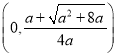 上单调增,在
上单调增,在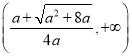 上单调减.
上单调减.
所以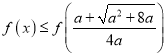 .………………………………………………10分
.………………………………………………10分
设![]() ,因为函数
,因为函数![]() 只有1个零点,而
只有1个零点,而![]() ,
,
所以![]() 是函数
是函数![]() 的唯一零点.
的唯一零点.
当![]() 时,
时, ![]() ,
, ![]() 有且只有
有且只有![]() 个零点,
个零点,
此时![]() ,解得
,解得![]() .…………………………………………12分
.…………………………………………12分
下证,当![]() 时,
时, ![]() 的零点不唯一.
的零点不唯一.
若![]() ,则
,则![]() ,此时
,此时![]() ,即
,即![]() ,则
,则![]() .
.
由(2)知, ![]() ,又函数
,又函数![]() 在以
在以![]() 和
和![]() 为端点的闭区间上的图象不间断,
为端点的闭区间上的图象不间断,
所以在![]() 和
和![]() 之间存在
之间存在![]() 的零点,则
的零点,则![]() 共有2个零点,不符合题意;
共有2个零点,不符合题意;
若![]() ,则
,则![]() ,此时
,此时![]() ,即
,即![]() ,则
,则![]() .
.
同理可得,在![]() 和
和![]() 之间存在
之间存在![]() 的零点,则
的零点,则![]() 共有2个零点,不符合题意.
共有2个零点,不符合题意.
因此![]() ,所以
,所以![]() 的值为
的值为![]() .…………………………………………………16分
.…………………………………………………16分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三文科
 名学生参加了
名学生参加了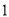 月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机数表法从中抽取
月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机数表法从中抽取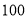 名学生的成绩进行统计分析,抽出的
名学生的成绩进行统计分析,抽出的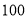 名学生的数学、语文成绩如下表.
名学生的数学、语文成绩如下表.
(1)将学生编号为:
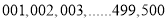 , 若从第
, 若从第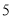 行第
行第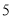 列的数开始右读,请你依次写出最先抽出的
列的数开始右读,请你依次写出最先抽出的 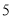 个人的编号(下面是摘自随机用表的第四行至第七行)
个人的编号(下面是摘自随机用表的第四行至第七行)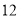
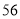
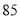



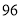
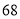
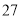
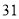
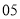
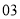
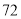

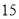
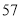
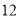
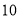
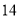
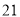
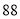
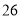
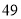

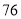

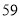
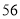


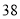
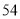
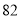
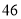
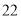
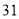
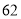
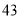
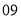

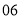
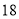
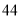


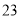

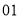
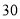
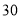
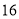
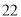

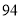
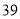
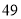
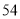
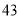
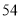
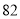


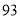
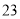
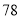
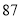
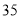
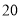
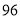

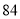
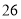
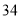
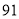
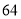
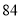
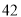
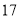
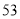


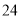
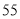

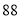
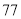
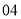



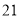

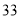


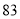
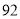
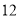

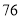
(2)若数学优秀率为
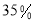 ,求
,求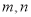 的值;
的值;(3)在语文成绩为良的学生中,已知
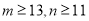 ,求数学成绩“优”比“良”的人数少的概率.
,求数学成绩“优”比“良”的人数少的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点为
的焦点为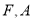 为
为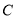 上异于原点的任意一点,过点
上异于原点的任意一点,过点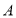 的直线
的直线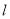 交
交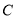 于另一点
于另一点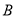 ,交
,交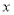 轴的正半轴于点
轴的正半轴于点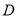 ,且有
,且有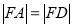 .当点
.当点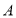 横坐标为
横坐标为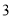 时,
时,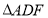 为正三角形.
为正三角形.(1)求
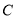 的方程;
的方程;(2)若直线
 ,且
,且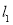 和
和 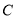 有且只有一个公共点
有且只有一个公共点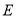 .
.①证明直线
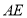 过定点,并求出定点坐标;
过定点,并求出定点坐标;②
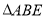 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
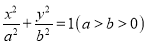 的左、右焦点分别为
的左、右焦点分别为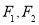 ,右顶点为
,右顶点为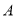 ,上顶点为
,上顶点为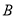 ,已知
,已知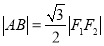 .
.(1)求椭圆的离心率;
(2)设
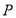 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段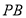 为直径的圆经过点
为直径的圆经过点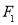 ,经过原点
,经过原点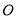 的直线
的直线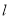 与该圆相切,求直线
与该圆相切,求直线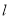 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知抛物线
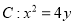 ,过点
,过点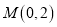 任作一直线与
任作一直线与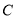 相交于
相交于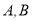 两点,过点
两点,过点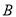 作
作 轴的平行线与直线
轴的平行线与直线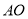 相交于点
相交于点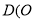 为坐标原点).
为坐标原点).(1)证明: 动点
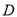 在定直线上;
在定直线上;(2)作
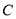 的任意一条切线
的任意一条切线 (不含
(不含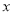 轴), 与直线
轴), 与直线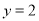 相交于点
相交于点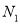 与(1)中的定直线相交于点
与(1)中的定直线相交于点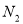 .
.证明:
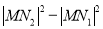 为定值, 并求此定值.
为定值, 并求此定值.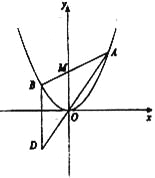
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数列
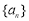 中,已知
中,已知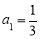 ,
,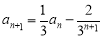 ,
,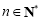 ,设
,设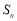 为
为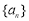 的前
的前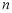 项和.
项和.(1)求证:数列
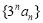 是等差数列;
是等差数列;(2)求
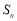 ;
;(3)是否存在正整数
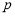 ,
,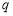 ,
,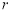
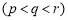 ,使
,使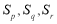 成等差数列?若存在,求出
成等差数列?若存在,求出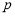 ,
,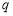 ,
,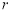 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 平面
平面 ,
, ,
,  ,
,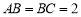 ,
, 为
为 的中点.
的中点.(1)求异面直线
 ,
, 所成角的余弦值;
所成角的余弦值;(2)点
 在线段
在线段 上,且
上,且 ,若直线
,若直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.
相关试题

