【题目】已知抛物线![]() 的焦点为
的焦点为![]() 为
为![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 横坐标为
横坐标为![]() 时,
时,![]() 为正三角形.
为正三角形.
(1)求![]() 的方程;
的方程;
(2)若直线![]() ,且
,且![]() 和
和 ![]() 有且只有一个公共点
有且只有一个公共点![]() .
.
①证明直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
②![]() 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)①证明见解析,
;(2)①证明见解析,![]() ;②存在,
;②存在,![]() .
.
【解析】
试题分析:(1)根据抛物线的焦半径公式,结合等边三角形的性质,求出![]() 的值,即可求解抛物线的方程;(2)①设出点
的值,即可求解抛物线的方程;(2)①设出点![]() 的坐标,求出直线
的坐标,求出直线![]() 的方程,利用
的方程,利用![]() ,且
,且![]() 和
和![]() 有且只有一个公共点
有且只有一个公共点![]() ,求出点
,求出点![]() 的坐标,写出直线
的坐标,写出直线![]() 的方程,将方程化为点斜式,即可求解定点的坐标;②中由①知直线
的方程,将方程化为点斜式,即可求解定点的坐标;②中由①知直线![]() 过焦点
过焦点![]() ,所以
,所以![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,再由直线的点斜式,利用点到直线的距离公式,再利用基本不等式即可求解结论.
,再由直线的点斜式,利用点到直线的距离公式,再利用基本不等式即可求解结论.
试题解析:(1)由题意知![]() ,设
,设![]() ,则
,则![]() 的中点为
的中点为![]() ,因为
,因为![]() ,由抛物线的定义知
,由抛物线的定义知![]() ,解得
,解得![]() 或
或![]() (舍去).由
(舍去).由![]() ,解得
,解得![]() ,所以抛物线
,所以抛物线![]() 的方程为
的方程为![]() .
.
(2)①证明:由(1)知![]() ,设
,设![]() ,因为
,因为![]() ,则
,则![]() ,由
,由![]() 得,
得,![]() ,故
,故![]() ,故直线
,故直线![]() 的斜率
的斜率![]() ,因为直线
,因为直线![]() 和直线
和直线![]() 平行,设直线
平行,设直线![]() 的方程为
的方程为![]() ,代人抛物线的方程得
,代人抛物线的方程得![]() ,由题意
,由题意![]() ,得
,得![]() ,设
,设![]() ,则
,则![]() ,当
,当![]() 时,
时,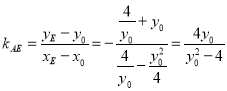 ,可得直线
,可得直线![]() 的方程为
的方程为![]() ,由
,由![]() ,整理可得
,整理可得![]() ,直线
,直线![]() 恒过点
恒过点![]() .当
.当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,过点
,过点![]() .所以直线
.所以直线![]() 过定点
过定点![]() .
.
②由①知直线![]() 过焦点
过焦点![]() ,所以
,所以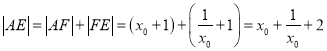 .设直线
.设直线![]() 的方程为
的方程为![]() ,因为点
,因为点![]() 在直线
在直线![]() 上,故
上,故![]() ,设
,设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,由
,由![]() ,得
,得![]() ,代人抛物线的方程得
,代人抛物线的方程得![]() ,所以
,所以![]() ,可求得
,可求得![]() .所以点
.所以点![]() 到直线
到直线![]() 的距离为
的距离为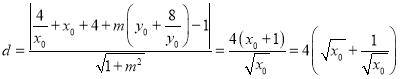 ,则
,则![]() 的面积
的面积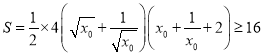 ,当且仅当
,当且仅当![]() ,即
,即![]() 时,等号成立.所以
时,等号成立.所以![]() 的面积的最小值为
的面积的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】时下,租车已经成为新一代的流行词,租车自驾游也慢慢流行起来,某小车租车点的收费标准是,不超过2天按照300元计算;超过两天的部分每天收费标准为100元(不足1天的部分按1天计算).有甲乙两人相互独立来该租车点租车自驾游(各租一车一次),设甲、乙不超过2天还车的概率分别为
 ;2天以上且不超过3天还车的概率分别
;2天以上且不超过3天还车的概率分别 ;两人租车时间都不会超过4天.
;两人租车时间都不会超过4天.(1)求甲所付租车费用大于乙所付租车费用的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量
 ,求
,求 的分布列与数学期望
的分布列与数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,其中
,其中 .
.(1)若
 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;(2)求
 的单调区间;
的单调区间;(3)若
 在
在 上的最大值是0,求
上的最大值是0,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三文科
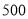 名学生参加了
名学生参加了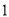 月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机数表法从中抽取
月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机数表法从中抽取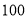 名学生的成绩进行统计分析,抽出的
名学生的成绩进行统计分析,抽出的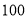 名学生的数学、语文成绩如下表.
名学生的数学、语文成绩如下表.
(1)将学生编号为:
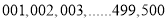 , 若从第
, 若从第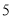 行第
行第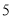 列的数开始右读,请你依次写出最先抽出的
列的数开始右读,请你依次写出最先抽出的 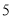 个人的编号(下面是摘自随机用表的第四行至第七行)
个人的编号(下面是摘自随机用表的第四行至第七行)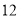
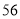
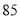



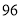
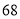
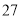
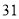
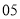
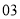
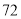

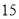
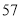
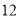
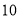
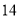
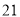
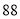
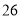
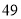

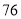

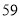
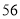


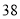
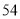
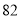
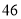
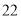
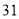
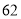
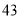
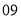

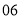
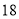
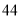


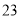

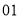
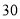
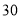
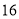
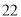

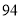
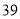
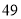
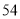
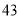
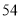
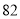


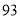
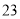
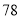
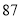
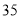
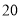
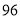

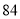
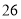
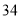
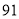
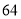
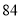
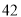
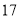
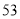


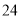
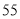

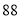
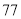
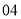



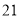

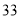


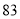
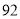

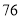
(2)若数学优秀率为
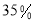 ,求
,求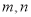 的值;
的值;(3)在语文成绩为良的学生中,已知
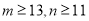 ,求数学成绩“优”比“良”的人数少的概率.
,求数学成绩“优”比“良”的人数少的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
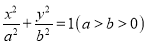 的左、右焦点分别为
的左、右焦点分别为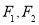 ,右顶点为
,右顶点为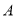 ,上顶点为
,上顶点为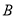 ,已知
,已知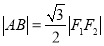 .
.(1)求椭圆的离心率;
(2)设
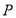 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段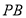 为直径的圆经过点
为直径的圆经过点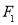 ,经过原点
,经过原点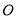 的直线
的直线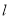 与该圆相切,求直线
与该圆相切,求直线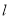 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
,  为正实数.
为正实数.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)求证:
 ;
;(3)若函数
 有且只有
有且只有 个零点,求
个零点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知抛物线
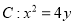 ,过点
,过点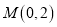 任作一直线与
任作一直线与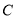 相交于
相交于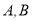 两点,过点
两点,过点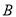 作
作 轴的平行线与直线
轴的平行线与直线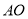 相交于点
相交于点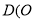 为坐标原点).
为坐标原点).(1)证明: 动点
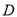 在定直线上;
在定直线上;(2)作
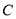 的任意一条切线
的任意一条切线 (不含
(不含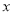 轴), 与直线
轴), 与直线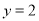 相交于点
相交于点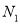 与(1)中的定直线相交于点
与(1)中的定直线相交于点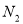 .
.证明:
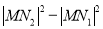 为定值, 并求此定值.
为定值, 并求此定值.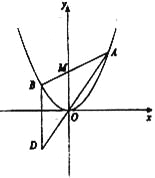
相关试题

