【题目】在数列![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,设
,设![]() 为
为![]() 的前
的前![]() 项和.
项和.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)求![]() ;
;
(3)是否存在正整数![]() ,
,![]() ,
,![]()
![]() ,使
,使![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() ,
,![]() ,
,![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(1)详见解析(2)![]() (3)
(3)![]() ,
,![]() ,
,![]() 的值为
的值为![]() ,
,![]() ,
,![]() .
.
【解析】
试题分析:(1)证明数列为等差数列,一般方法为定义法,即利用相邻两项的差为常数进行论证:![]() (2)先确定
(2)先确定![]() 的通项公式:
的通项公式:![]() ,再求
,再求![]() ,最后利用错位相减法求和,注意相减时项的符号变化、项数的确定、最后结果得表示(3)存在性问题,一般以算代探:先根据
,最后利用错位相减法求和,注意相减时项的符号变化、项数的确定、最后结果得表示(3)存在性问题,一般以算代探:先根据![]() 成等差数列得
成等差数列得![]() ,代入得
,代入得![]() ,通过研究
,通过研究![]() 单调性,确定满足条件解的范围:当
单调性,确定满足条件解的范围:当![]() 时
时![]() ,因此满足条件的解
,因此满足条件的解![]() ,经验证满足条件
,经验证满足条件
试题解析:(1)证明:因为![]() ,所以
,所以![]() ,…………………2分
,…………………2分
又因为![]() ,所以
,所以![]() ,
,
所以![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列. …………………………4分
的等差数列. …………………………4分
(2)由(1)知![]() ,所以
,所以![]() ,………6分
,………6分
所以![]() ,
,
所以![]() ,
,
两式相减得![]()
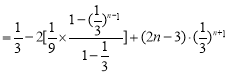
![]() ,
,
所以![]() .…………………………………………………………………10分
.…………………………………………………………………10分
(3)假设存在正整数![]() ,
,![]() ,
,![]()
![]() ,使
,使![]() 成等差数列,
成等差数列,
则![]() ,即
,即![]() .
.
由于当![]() 时,
时,![]() ,所以数列
,所以数列![]() 单调递减.
单调递减.
又![]() ,所以
,所以![]() 且
且![]() 至少为2,所以
至少为2,所以![]() , ………………12分
, ………………12分
![]() .
.
①当![]() 时,
时,![]() ,又
,又![]() ,
,
所以![]() ,等式不成立.………………………………………14分
,等式不成立.………………………………………14分
②当![]() 时,
时,![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() (
(![]() 单调递减,解唯一确定).
单调递减,解唯一确定).
综上可知,![]() ,
,![]() ,
,![]() 的值为
的值为![]() ,
,![]() ,
,![]() . ………………………………16分
. ………………………………16分
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
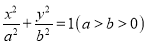 的左、右焦点分别为
的左、右焦点分别为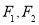 ,右顶点为
,右顶点为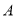 ,上顶点为
,上顶点为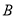 ,已知
,已知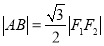 .
.(1)求椭圆的离心率;
(2)设
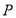 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段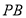 为直径的圆经过点
为直径的圆经过点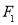 ,经过原点
,经过原点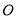 的直线
的直线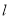 与该圆相切,求直线
与该圆相切,求直线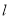 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
,  为正实数.
为正实数.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)求证:
 ;
;(3)若函数
 有且只有
有且只有 个零点,求
个零点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知抛物线
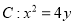 ,过点
,过点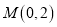 任作一直线与
任作一直线与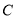 相交于
相交于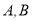 两点,过点
两点,过点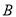 作
作 轴的平行线与直线
轴的平行线与直线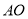 相交于点
相交于点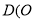 为坐标原点).
为坐标原点).(1)证明: 动点
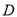 在定直线上;
在定直线上;(2)作
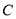 的任意一条切线
的任意一条切线 (不含
(不含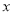 轴), 与直线
轴), 与直线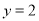 相交于点
相交于点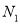 与(1)中的定直线相交于点
与(1)中的定直线相交于点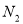 .
.证明:
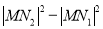 为定值, 并求此定值.
为定值, 并求此定值.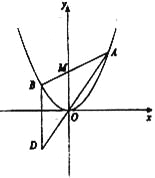
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 平面
平面 ,
, ,
,  ,
,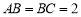 ,
, 为
为 的中点.
的中点.(1)求异面直线
 ,
, 所成角的余弦值;
所成角的余弦值;(2)点
 在线段
在线段 上,且
上,且 ,若直线
,若直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市有一直角梯形绿地
 ,其中
,其中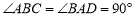 ,
, km,
km,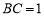 km.现过边界
km.现过边界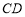 上的点
上的点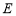 处铺设一条直的灌溉水管
处铺设一条直的灌溉水管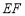 ,将绿地分成面积相等的两部分.
,将绿地分成面积相等的两部分.(1)如图①,若
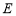 为
为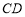 的中点,
的中点,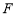 在边界
在边界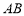 上,求灌溉水管
上,求灌溉水管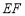 的长度;
的长度;(2)如图②,若
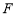 在边界
在边界 上,求灌溉水管
上,求灌溉水管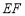 的最短长度.
的最短长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四棱锥
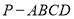 中,底面
中,底面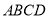 是正方形,
是正方形,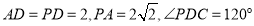 .
.(1)如图2,设点
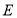 为
为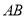 的中点,点
的中点,点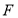 为
为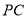 的中点,求证:
的中点,求证: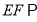 平面
平面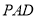 ;
;(2)已知网格纸上小正方形的边长为
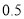 ,请你在网格纸上用粗线画图1中四棱锥
,请你在网格纸上用粗线画图1中四棱锥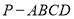 的府视图(不需要标字母),并说明理由.
的府视图(不需要标字母),并说明理由.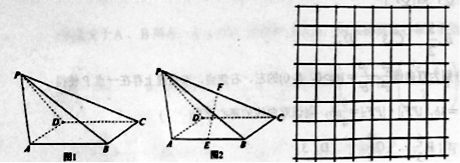
相关试题

