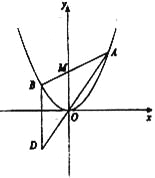
【题目】如图所示,已知抛物线![]() ,过点
,过点![]() 任作一直线与
任作一直线与![]() 相交于
相交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() 为坐标原点).
为坐标原点).
(1)证明: 动点![]() 在定直线上;
在定直线上;
(2)作![]() 的任意一条切线
的任意一条切线![]() (不含
(不含![]() 轴), 与直线
轴), 与直线![]() 相交于点
相交于点![]() 与(1)中的定直线相交于点
与(1)中的定直线相交于点![]() .
.
证明: ![]() 为定值, 并求此定值.
为定值, 并求此定值.
参考答案:
【答案】(1)证明见解析;(2)证明见解析, ![]() .
.
【解析】试题分析:(1)依题意可设![]() 的方程为
的方程为![]() ,代人
,代人![]() ,得即
,得即![]() ,设
,设![]() ,则有
,则有![]() ,直线
,直线![]() 的方程为
的方程为![]() 的方程为
的方程为![]() ,解得交点
,解得交点![]() 的坐标,利用
的坐标,利用![]() ,即可求得
,即可求得![]() 点在定直线
点在定直线![]() 上;(2)依据题意得,切线
上;(2)依据题意得,切线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得即
得即![]() .由
.由![]() 得
得![]() ,分别令
,分别令![]() 得得
得得![]() 的坐标为
的坐标为![]() ,从而可知
,从而可知![]() 为定值.
为定值.
试题解析:(1)依题意可设![]() 的方程为
的方程为![]() ,代人
,代人![]() ,得
,得![]() ,
,
即![]() ,设
,设![]() ,则有
,则有![]() ,
,
直线![]() 的方程为
的方程为![]() 的方程为
的方程为![]() ,解得交点
,解得交点![]() 的坐标为
的坐标为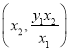 ,
,
注意到![]() 及
及![]() ,则有
,则有![]() ,
,
因此![]() 点在定直线
点在定直线![]() 上
上![]() .
.
(2)依题意,切线![]() 的斜率存在且不等于
的斜率存在且不等于![]() .
.
设切线![]() 的方程为
的方程为![]() ,代人
,代人![]() 得
得![]() ,即
,即![]() .
.
由![]() 得
得![]() ,化简整理得
,化简整理得![]() .故切线
.故切线![]() 的方程可写为
的方程可写为![]() .
.
分别令![]() ,得
,得![]() 的坐标为
的坐标为![]() ,
,
则![]() ,即
,即![]() 为定值
为定值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点为
的焦点为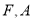 为
为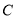 上异于原点的任意一点,过点
上异于原点的任意一点,过点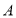 的直线
的直线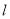 交
交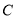 于另一点
于另一点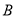 ,交
,交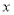 轴的正半轴于点
轴的正半轴于点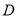 ,且有
,且有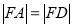 .当点
.当点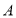 横坐标为
横坐标为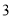 时,
时,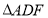 为正三角形.
为正三角形.(1)求
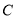 的方程;
的方程;(2)若直线
 ,且
,且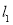 和
和 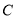 有且只有一个公共点
有且只有一个公共点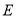 .
.①证明直线
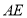 过定点,并求出定点坐标;
过定点,并求出定点坐标;②
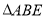 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
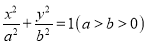 的左、右焦点分别为
的左、右焦点分别为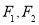 ,右顶点为
,右顶点为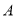 ,上顶点为
,上顶点为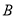 ,已知
,已知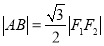 .
.(1)求椭圆的离心率;
(2)设
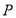 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段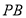 为直径的圆经过点
为直径的圆经过点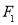 ,经过原点
,经过原点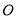 的直线
的直线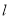 与该圆相切,求直线
与该圆相切,求直线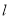 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
,  为正实数.
为正实数.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)求证:
 ;
;(3)若函数
 有且只有
有且只有 个零点,求
个零点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列
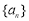 中,已知
中,已知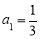 ,
,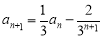 ,
,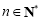 ,设
,设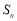 为
为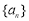 的前
的前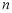 项和.
项和.(1)求证:数列
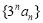 是等差数列;
是等差数列;(2)求
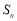 ;
;(3)是否存在正整数
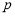 ,
,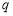 ,
,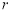
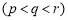 ,使
,使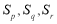 成等差数列?若存在,求出
成等差数列?若存在,求出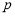 ,
,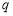 ,
,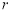 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 平面
平面 ,
, ,
,  ,
,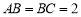 ,
, 为
为 的中点.
的中点.(1)求异面直线
 ,
, 所成角的余弦值;
所成角的余弦值;(2)点
 在线段
在线段 上,且
上,且 ,若直线
,若直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市有一直角梯形绿地
 ,其中
,其中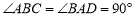 ,
, km,
km,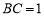 km.现过边界
km.现过边界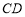 上的点
上的点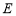 处铺设一条直的灌溉水管
处铺设一条直的灌溉水管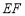 ,将绿地分成面积相等的两部分.
,将绿地分成面积相等的两部分.(1)如图①,若
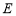 为
为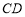 的中点,
的中点,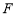 在边界
在边界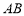 上,求灌溉水管
上,求灌溉水管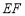 的长度;
的长度;(2)如图②,若
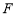 在边界
在边界 上,求灌溉水管
上,求灌溉水管 的最短长度.
的最短长度.
相关试题

